
Full resolution (JPEG) - On this page / på denna sida - Sidor ...
<< prev. page << föreg. sida << >> nästa sida >> next page >>
Below is the raw OCR text
from the above scanned image.
Do you see an error? Proofread the page now!
Här nedan syns maskintolkade texten från faksimilbilden ovan.
Ser du något fel? Korrekturläs sidan nu!
This page has never been proofread. / Denna sida har aldrig korrekturlästs.
Teknisk Tidskrift
FIÉ
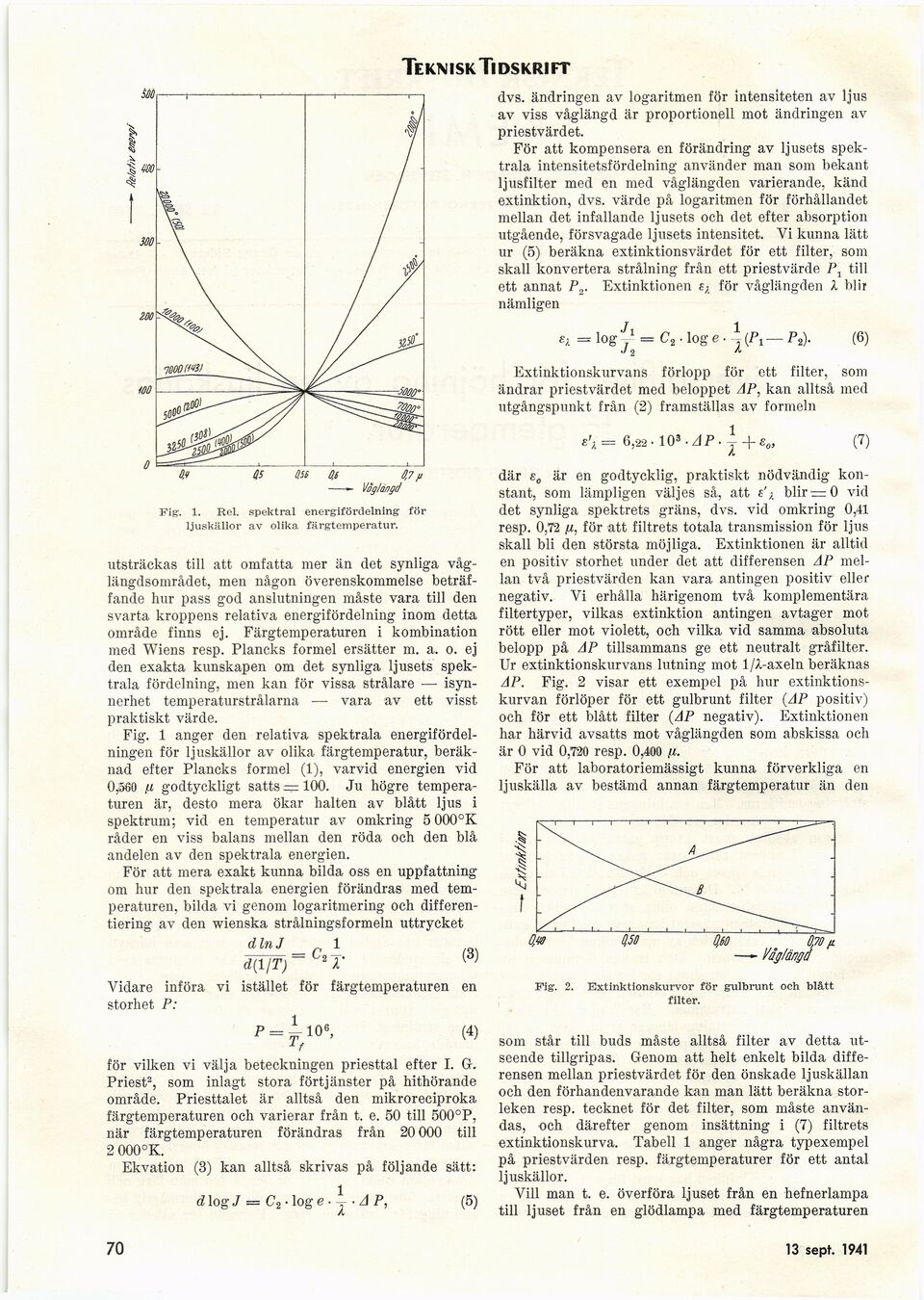
1. Rel. spektral energifördelning för
ljuskällor av olika färgtemperatur.
utsträckas till att omfatta mer än det synliga
våglängdsområdet, men någon överenskommelse
beträffande hur pass god anslutningen måste vara till den
svarta kroppens relativa energifördelning inom detta
område finns ej. Färgtemperaturen i kombination
med Wiens resp. Plancks formel ersätter m. a. o. ej
den exakta kunskapen om det synliga ljusets
spektrala fördelning, men kan för vissa strålare —
isynnerhet temperaturstrålarna — vara av ett visst
praktiskt värde.
Fig. 1 anger den relativa spektrala
energifördelningen för ljuskällor av olika färgtemperatur,
beräknad efter Plancks formel (1), varvid energien vid
OpöO fi godtyckligt satts == 100. Ju högre
temperaturen är, desto mera ökar halten av blått ljus i
spektrum; vid en temperatur av omkring 5 000°K
råder en viss balans mellan den röda och den blå
andelen av den spektrala energien.
För att mera exakt kunna bilda oss en uppfattning
om hur den spektrala energien förändras med
temperaturen, bilda vi genom logaritmering och
differentiering av den wienska strålningsformeln uttrycket
dlnJ 1
d[ljf) = 2 T
Vidare införa vi istället för färgtemperaturen en
storhet P:
p = (4)
för vilken vi välja beteckningen priesttal efter I. G-.
Priest2, som inlagt stora förtjänster på hithörande
område. Priesttalet är alltså den mikroreciproka
färgtemperaturen och varierar från t. e. 50 till 500°P,
när färgtemperaturen förändras från 20 000 till
2 000°K.
Ekvation (3) kan alltså skrivas på följande sätt:
dvs. ändringen av logaritmen för intensiteten av ljus
av viss våglängd är proportionell mot ändringen av
priestvärdet.
För att kompensera en förändring av ljusets
spektrala intensitetsfördelning använder man som bekant
ljusfilter med en med våglängden varierande, känd
extinktion, dvs. värde på logaritmen för förhållandet
mellan det infallande ljusets och det efter absorption
utgående, försvagade ljusets intensitet. Vi kunna lätt
ur (5) beräkna extinktionsvärdet för ett filter, som
skall konvertera strålning från ett priestvärde P1 till
ett annat P2. Extinktionen f; för våglängden X blir
nämlisren
s,_ = log ~ = C2
J •>
loge- ,(Pi— Pt).
(6)
Extinktionskurvans förlopp för ett filter, som
ändrar priestvärdet med beloppet AP, kan alltså med
utgångspunkt från (2) framställas av formeln
s\= 6,22-103-AP.j+e0,
CO
där s0 är en godtycklig, praktiskt nödvändig
konstant, som lämpligen väljes så, att e’x blir = 0 vid
det synliga spektrets gräns, dvs. vid omkring 0,41
resp. 0,72 fi, för att filtrets totala transmission för ljus
skall bli den största möjliga. Extinktionen är alltid
en positiv storhet under det att differensen AP
mellan två priestvärden kan vara antingen positiv eller
negativ. Vi erhålla härigenom två komplementära
filtertyper, vilkas extinktion antingen avtager mot
rött eller mot violett, och vilka vid samma absoluta
belopp på AP tillsammans ge ett neutralt gråfilter.
Ur extinktionskurvans lutning mot 1/A-axeln beräknas
AP. Fig. 2 visar ett exempel på hur
extinktions-kurvan förlöper för ett gulbrunt filter (AP positiv)
och för ett blått filter (AP negativ). Extinktionen
har härvid avsatts mot våglängden som abskissa och
är 0 vid 0,720 resp. 0,400 fi.
För att laboratoriemässigt kunna förverkliga en
ljuskälla av bestämd annan färgtemperatur än den
1
a
(3)
d log J = C2 • log e ■ T ■ A P,
A
(5)
Fig. 2. Extinktionskurvor för gulbrunt och blått
filter.
som står till buds måste alltså filter av detta
utseende tillgripas. Genom att helt enkelt bilda
differensen mellan priestvärdet för den önskade ljuskällan
och den förhandenvarande kan man lätt beräkna
storleken resp. tecknet för det filter, som måste
användas, och därefter genom insättning i (7) filtrets
extinktionskurva. Tabell 1 anger några typexempel
på priestvärden resp. färgtemperaturer för ett antal
ljuskällor.
Vill man t. e. överföra ljuset från en hefnerlampa
till ljuset från en glödlampa med färgtemperaturen
70
13 sept. 1941
<< prev. page << föreg. sida << >> nästa sida >> next page >>