
Full resolution (JPEG) - On this page / på denna sida - Sidor ...
<< prev. page << föreg. sida << >> nästa sida >> next page >>
Below is the raw OCR text
from the above scanned image.
Do you see an error? Proofread the page now!
Här nedan syns maskintolkade texten från faksimilbilden ovan.
Ser du något fel? Korrekturläs sidan nu!
This page has never been proofread. / Denna sida har aldrig korrekturlästs.
VÄG. OCH VATTENBYGGNADSKONST SAMT HUSBYGGNADSTEKNIK
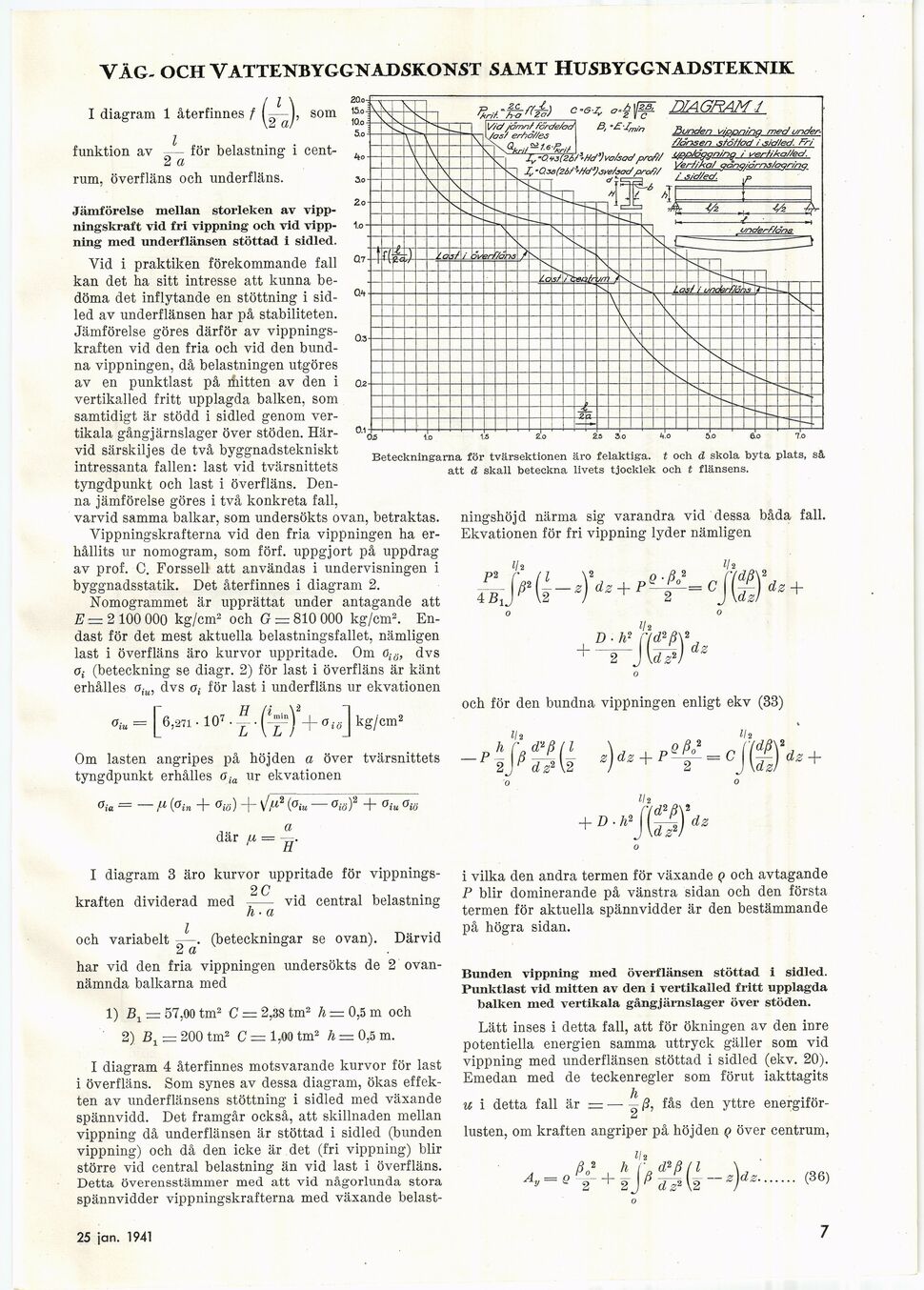
I diagram 1 återfinnes †
l
2 a
rum, överfläns och underfläns.
som
funktion av
(2 J’
för belastning i cent-
Jämförelse mellan storleken av
vipp-ningskraft vid fri vippning och vid
vipp-ning med underflänsen stöttad i sidled.
Yid i praktiken förekommande fall
kan det ha sitt intresse att kunna
bedöma det inflytande en stöttning i
sidled av underflänsen har på stabiliteten.
Jämförelse göres därför av
vippnings-kraften vid den fria och vid den
bundna vippningen, då belastningen utgöres
av en punktlast på diitten av den i
vertikalled fritt upplagda balken, som
samtidigt är stödd i sidled genom
vertikala gångjärnslager över stöden.
Härvid särskiljes de två byggnadstekniskt
intressanta fallen: last vid tvärsnittets
tyngdpunkt och last i överfläns.
Denna jämförelse göres i två konkreta fall,
varvid samma balkar, som undersökts ovan, betraktas.
Yippningskrafterna vid den fria vippningen ha
erhållits ur nomogram, som förf. uppgjort på uppdrag
av prof. C. Forssell att användas i undervisningen i
byggnadsstatik. Det återfinnes i diagram 2.
Nomogrammet är upprättat under antagande att
£ = 2 100 000 kg/cm2 och G — 810 000 kg/cm2.
Endast för det mest aktuella belastningsfallet, nämligen
last i överfläns äro kurvor uppritade. Om oiö) dvs
Oi (beteckning se diagr. 2) för last i överfläns är känt
erhålles af.
Beteckningarna för tvärsektionen äro felaktiga, t och d skola byta plats,
att d skall beteckna livets tjocklek och t flänsens.
ningshöjd närma sig varandra vid dessa båda fall.
Ekvationen för fri vippning lyder nämligen
P2
4 Bi,
ih
o
z dz + P
Q-I
-= C
dß
d
dz
+
D ■ h2
il 2
m
dz
0;„ =
iu, dvs a; för last i underfläns ur ekvationen
H ii„
6,271- 107-
öiö] kg/cm2
och för den bundna vippningen enligt ekv (33)
Om lasten angripes på höjden a över tvärsnittets
tyngdpunkt erhålles oia ur ekvationen
— P
d*ß ti
cTzA 2
z]dz + P
Qßo2
dz-f
»ia = — {Oin + Ö;ö) + VV2 (°iu — Oiöf + Oiu Oiö
där [j, = (’rr.
H
I diagram 3 äro kurvor uppritade för
vippnings-2 C
kraften dividerad med —— vid central belastning
h ■ a
D ■ A2
m
dz
och variabelt
l
2 a
(beteckningar se ovan). Därvid
har vid den fria vippningen undersökts de 2
ovannämnda balkarna med
1) B1 — 57,00 tm2 C — 2,38 tm2 h = 0,5 m och
2) B1 = 200 tm2 C = 1,00 tm2 h = 0,5 m.
I diagram 4 återfinnes motsvarande kurvor för last
i överfläns. Som synes av dessa diagram, ökas
effekten av underflänsens stöttning i sidled med växande
spännvidd. Det framgår också, att skillnaden mellan
vippning då underflänsen är stöttad i sidled (bunden
vippning) och då den icke är det (fri vippning) blir
större vid central belastning än vid last i överfläns.
Detta överensstämmer med att vid någorlunda stora
spännvidder vippningskrafterna med växande belast-
i vilka den andra termen för växande q och avtagande
P blir dominerande på vänstra sidan och den första
termen för aktuella spännvidder är den bestämmande
på högra sidan.
Bunden vippning med överflänsen stöttad i sidled.
Punktlast vid mitten av den i vertikalled fritt upplagda
balken med vertikala gångjärnslager över stöden.
Lätt inses i detta fall, att för ökningen av den inre
potentiella energien samma uttryck gäller som vid
vippning med underflänsen stöttad i sidled (ekv. 20).
Emedan med de teckenregler som förut iakttagits
w i detta fall är = —- ^ ß, fås den yttre energiför-
Lt
lusten, om kraften angriper på höjden q över centrum,
A„
ß02
il 2
h i-dtßfl
2 JP dz2 \2
■ z ]dz.
(36)
25 jan. 1941
.7
<< prev. page << föreg. sida << >> nästa sida >> next page >>