
Full resolution (JPEG) - On this page / på denna sida - H. 19. 11 maj 1946 - Värmespänningar i ringar, rör och skivor, av Lars Nordström
<< prev. page << föreg. sida << >> nästa sida >> next page >>
Below is the raw OCR text
from the above scanned image.
Do you see an error? Proofread the page now!
Här nedan syns maskintolkade texten från faksimilbilden ovan.
Ser du något fel? Korrekturläs sidan nu!
This page has never been proofread. / Denna sida har aldrig korrekturlästs.
11 maj 1946
479
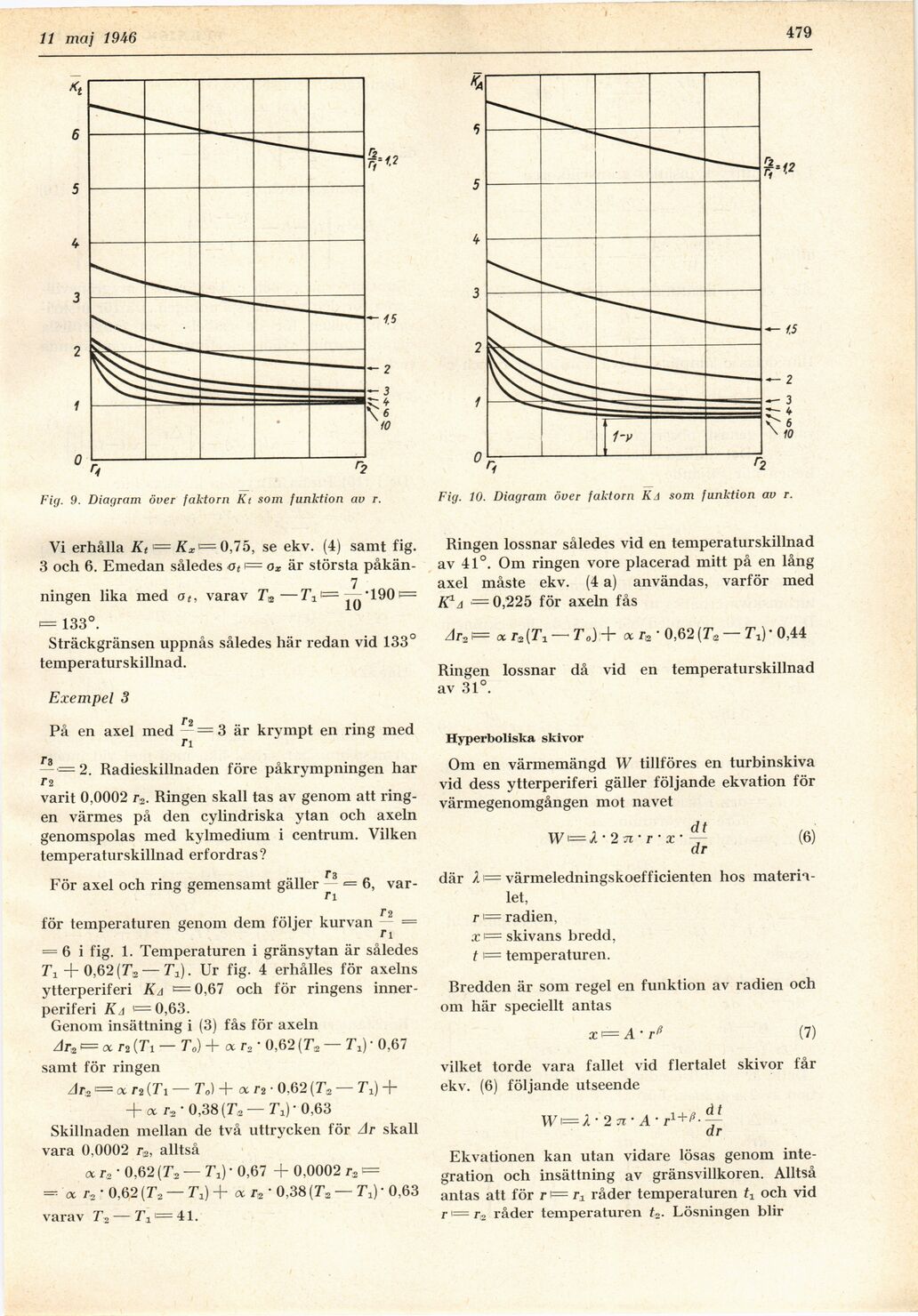
Fig. 9. Diagram över faktorn Kt som funktion av r.
Fig. 10. Diagram över faktorn ka som funktion av r.
Vi erhålla Kt <= Kx<= 0,75, se ekv. (4) samt fig.
3 och 6. Emedan således at r= ox är största påkän-
7
ningen lika med ot, varav T2—J1!’= ’190
i= 133°.
Sträckgränsen uppnås således här redan vid 133°
temperaturskillnad.
Exempel 3
t 2
På en axel med ^=3 är krvmpt en ring med
t i
t 3
t 2
2. Radieskillnaden före påkrympningen har
varit 0,0002 r2. Ringen skall tas av genom att
ringen värmes på den cylindriska ytan och axeln
genomspolas med kylmedium i centrum. Vilken
temperaturskillnad erfordras?
T3
För axel och ring gemensamt gäller — 6, var-
r i
J"2
för temperaturen genom dem följer kurvan - —
= 6 i fig. 1. Temperaturen i gränsytan är således
7\ + 0,62(r;2 — Tj). Ur fig. 4 erhålles för axelns
ytterperiferi Ka •= 0,67 och för ringens inner
-periferi Ka ^=0,63.
Genom insättning i (3) fås för axeln
Ar2 c=ocr2 (Ti — To)+oc r2 • 0,62 [Ta — Tx)’ 0,67
samt för ringen
At2 = a r2 (Ti — T0) + a r2 • 0.62 [Ta — Tx) +
+ a r2 ’ 0,38 (Ta — 7\)’ 0,63
Skillnaden mellan de två uttrycken för Ar skall
vara 0,0002 r2, alltså
a r2 • 0,62 [T2 — 7\) • 0,67 + 0,0002 r2 =
=■■ oc r2- 0,62[To — Tx) + a r2 ’ 0,38[T2 — 7\)• 0,63
varav T2 — Tx = 41.
Ringen lossnar således vid en temperaturskillnad
av 41°. Om ringen vore placerad mitt på en lång
axel måste ekv. (4 a) användas, varför med
K1 a =0,225 för axeln fås
Ars?= ocTv[Ti — To) + oc r,2’ 0,62 (Ta — 7\)* 0,44
Ringen lossnar då vid en temperaturskillnad
av 31°.
Hyperboliska skivor
Om en värmemängd W tillföres en turbinskiva
vid dess ytterperiferi gäller följande ekvation för
värmegenomgången mot navet
dt
dr
W i= X ’ 2 -n • r • x
(6)
där 11= värmeledningskoefficienten hos
materialet,
r i= radien,
xi= skivans bredd,
11= temperaturen.
Bredden är som regel en funktion av radien och
om här speciellt antas
x<=A-rß (7)
vilket torde vara fallet vid flertalet skivor får
ekv. (6) följande utseende
dt
W’=Å’ 2 Ji’ A’ r1+ß-
dr
Ekvationen kan utan vidare lösas genom
integration och insättning av gränsvillkoren. Alltså
antas att för r •= rx råder temperaturen och vid
r’=r2 råder temperaturen t2. Lösningen blir
<< prev. page << föreg. sida << >> nästa sida >> next page >>