
Full resolution (JPEG) - On this page / på denna sida - H. 25. 19 juni 1948 - Om den effekt, som vid segling utvinnes ur vinden, av Erik Petersohn
<< prev. page << föreg. sida << >> nästa sida >> next page >>
Below is the raw OCR text
from the above scanned image.
Do you see an error? Proofread the page now!
Här nedan syns maskintolkade texten från faksimilbilden ovan.
Ser du något fel? Korrekturläs sidan nu!
This page has never been proofread. / Denna sida har aldrig korrekturlästs.
12 juni 1948
403
Fitj. 5. Samboncl mellan
maximal vinkel från vinden och
olika v- och s-värden.
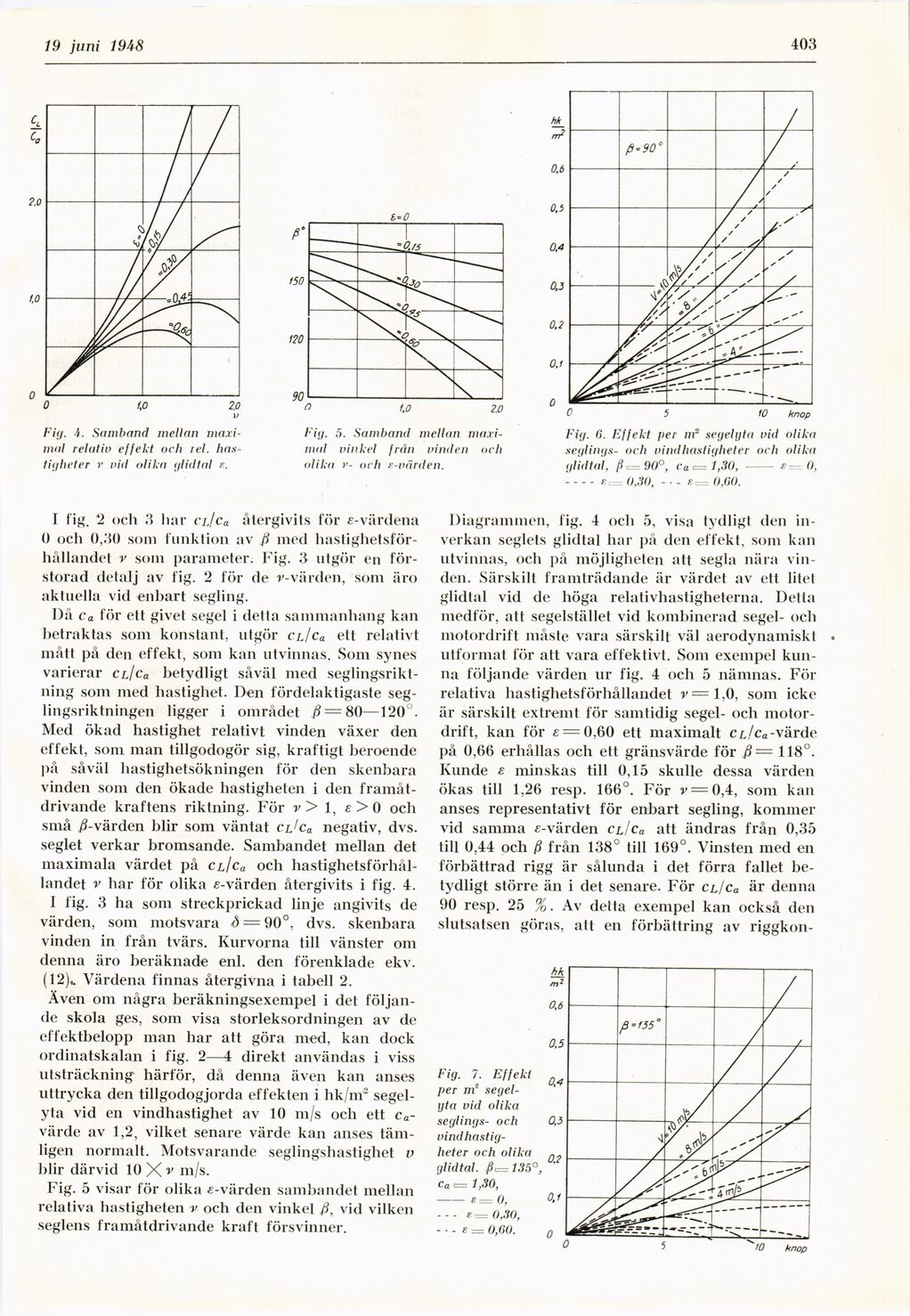
Fig. 0. Effekt per nr segehjta vid olika
seglings- och vindhastigheter och olika
glid tal, ß,= 90°, ca<=l,30, –O,
––£o,30, - ■ - f.= (),<><).
O
Fig. A. Samband mellan
maximal relativ effekt och rel.
hastigheter v vid olika glidtnl s.
I fig. 2 och 3 har cijca återgivits för e-värdena
0 och 0,30 som funktion av ß med
hastighetsförhållandet v som parameter. Fig. 3 utgör en
förstorad detalj av fig. 2 för de v-värden, som äro
aktuella vid enbart segling.
Då ca för elt givet segel i detta sammanhang kan
betraktas som konstant, utgör cl/cq ett relativt
mått på den effekt, som kan utvinnas. Som synes
varierar cl/cu betydligt såväl med
seglingsriktning som med hastighet. Den fördelaktigaste
seglingsriktningen ligger i området ß = H0—120 .
Med ökad hastighet relativt vinden växer den
effekt, som man tillgodogör sig, kraftigt beroende
på såväl hastighetsökningen för den skenbara
vinden som den ökade hastigheten i den
framåt-drivande kraftens riktning. För v> 1, £>0 och
små ß-värden blir som väntat cjca negativ, dvs.
seglet verkar bromsande. Sambandet mellan det
maximala värdet på clIcu och
hastighetsförhållandet v har för olika £-värden återgivits i fig. 4.
I fig. 3 ha som streckprickad linje angivits de
värden, som motsvara å = 90°, dvs. skenbara
vinden in från tvärs. Kurvorna till vänster om
denna äro beräknade enl. den förenklade ekv.
(12)fc Värdena finnas återgivna i tabell 2.
Även om några beräkningsexempel i det
följande skola ges, som visa storleksordningen av de
effektbelopp man har att göra med, kan dock
ordinatskalan i fig. 2—4 direkt användas i viss
utsträckning- härför, då denna även kan anses
uttrycka den tillgodogjorda effekten i hk/m2
segelyta vid en vindhastighet av 10 m/s och ett
ca-värde av 1,2, vilket senare värde kan anses
tämligen normalt. Motsvarande seglingshastighet v
blir därvid 10 X v m/s.
Fig. 5 visar för olika £-värden sambandet mellan
relativa hastigheten v och den vinkel ß, vid vilken
seglens framåtdrivande kraft försvinner.
Diagrammen, fig. 4 och 5, visa tydligt den
inverkan seglets glidtal har pä den effekt, som kan
utvinnas, och på möjligheten att segla nära
vinden. Särskilt framträdande är värdet av ett litel
glidtal vid de höga relativhastigheterna. Detta
medför, att segelstället vid kombinerad segel- och
motordrift måste vara särskilt väl aerodynamiskt •
utformat för att vara effektivt. Som exempel
kunna följande värden ur fig. 4 och 5 nämnas. För
relativa hastighetsförhållandet v =1.0, som icke
är särskilt extremt för samtidig segel- och
motordrift, kan för £ = 0,60 ett maximalt cl/cu-värde
på 0,66 erhållas och ett gränsvärde för ß= 118°.
Kunde s minskas till 0,15 skulle dessa värden
ökas till 1,26 resp. 166°. För v = 0,i, som kan
anses representativt för enbart segling, kommer
vid samma ^-värden clIco. att ändras från 0,35
till 0,44 och ß från 138° till 169°. Vinsten med en
förbättrad rigg är sålunda i det förra fallet
betydligt större än i det senare. För cl/Co. är denna
90 resp. 25 %. Av delta exempel kan också den
slutsatsen göras, att en förbättring av riggkon-
Fig. 7. Effekt
per m!
segelyta vid olika
seglings- och [-vindhastigheter-]
{+vindhastig-
heter+} och olika
glidtal. ßi==1350
ca i= 1,30,
- s = 0,
- - - t = 0,30,
- ■ - E — 0,60.
<< prev. page << föreg. sida << >> nästa sida >> next page >>