
Full resolution (JPEG) - On this page / på denna sida - H. 40. 4 november 1950 - Sannolikhetsberäkning av ledningsförlusters bidrag till toppenergier, av Jarl Salin
<< prev. page << föreg. sida << >> nästa sida >> next page >>
Below is the raw OCR text
from the above scanned image.
Do you see an error? Proofread the page now!
Här nedan syns maskintolkade texten från faksimilbilden ovan.
Ser du något fel? Korrekturläs sidan nu!
This page has never been proofread. / Denna sida har aldrig korrekturlästs.
11 november 1950
1005
Sannolikhetsberäkning
av ledningsförlusters bidrag
till toppenergier
Professor Jarl Salin, Åbo
519.2 : 621.311.153.22
Det problem, som här skall behandlas, uppkommer då
man för en ekonomisk jämförelse mellan olika
ledningsareor för en planerad kraftledning vill beräkna, vad
energi-förlusterna i denna kommer att kosta i form av avgifter
för bl.a. en ökad toppenergiförbrukning, om nämligen
energin köpes enligt en taxa, där en dylik
förbrukningsavgift förekommer, närmare bestämt för den med
subtraktionsmätare uppmätta toppenergi (VV, enligt
varaktighetsdiagrammet i fig. 1), som tas ut över en fastställd
subtraktionsgräns eller botteneffekt (I’s i fig. 1).
Problemet är tydligen ej alldeles enkelt ifall den
ifrågavarande ledningen överför ström till endast en del av de
förbrukningsapparater, till vilka energin inköpes. Då är
det t.ex. ej säkert att de stora ledningsförlusterna vid en
hög belastning i den förbrukargrupp, som ledningen
matar, alltid infaller under tider, då totalbelastningen
överstiger botteneffekten Ps och toppenergi registreras, ty det
kan eventuellt ibland även inträffa, att den övriga
förbrukningen i nätet vid dylika tillfällen är så låg, att
totaleffekten ej når upp till Ps.
Detta mera komplicerade problem kan — såsom här skall
visas — på ett relativt enkelt sätt utredas, ifall man
känner varaktighetskurvorna (fig. 2) för såväl den förbruk-
ning 1, vilken matas genom den ifrågavarande ledningen,
som för all den övriga, sammanlagda förbrukning 2, som
ingår i samma kraftinköp, och vidare kan räkna med att
dessa båda förbrukningar 1 och 2 under den betraktade
liden varierar stokastiskt oberoende au varandra.
Vi kan lämpligen- anta, att de givna varaktighetskurvorna
hänför sig till strömförbrukningarna och — därest fråga
är om växelströmmar — att alla strömmar är i fas med
varandra. Vi räknar vidare med att spänning och
effektfaktor vid effektmätningsstäilet är konstanta och kända,
så att där en fast proportionalitet mellan ström och effekt
erhålles. Ett enligt fig. 1 tänkt varaktighetsdiagram för
totaleffekten kan alltså tänkas försett även med en
gradering för strömmar. Den mot botteneffekten
(subtraktionsgränsen) Ps sålunda svarande strömmen betecknas i
det följande Is.
Grafisk pro blemlösn ing
Den problemlösning, som här skall beskrivas, ansluter sig
till en av mig angiven grafisk metod för beräkning av
varaktighetskurvan (fig. 1) för summaströmmen /x + /e
under de beskrivna förutsättningarna. Enligt denna metod,
vilken antas vara känd, uppritar man ett
"sammanlagrings-diagram" enligt fig. 3. För lösning av det nu föreliggande
problemet behöver man likväl ej rita upp alla de för
sain-manlagringsberäkningen nödiga kurvorna i
"sannolikhetskvadraten", utan endast den (i fig. 3 kraftigt tecknade)
kurva, som gäller för ett summavärde It 4- Ie lika med Is,
i fig. 3 enligt fig. 1 antaget lika med 8 kA.
Den i fig. 3 streckade yta, som omfattar
sannolikhetskvadratens högvärdeshörn och begränsas av Is-kurvan
samt av linjen för något värde Iu i fig. 3 som exempel
valt värdet 5 kA, visar sig ha en betydelse, som i detta
sammanhang är av intresse. Av den tankegång®, som ligger
till grund för en sammanlagringsberäkning enligt fig. 3,
framgår nämligen omedelbart, att denna streckade ytas
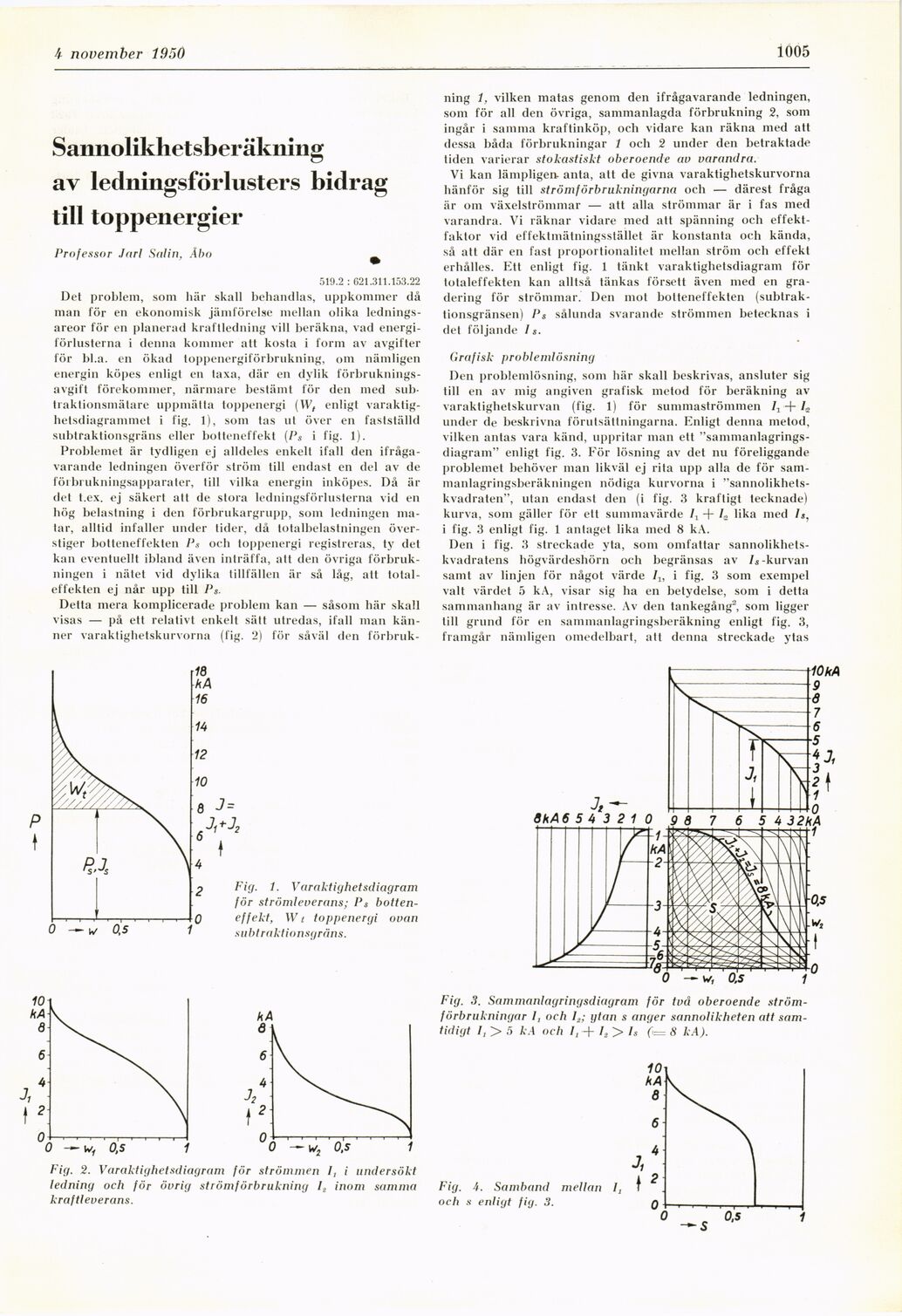
Fig. 3. Sammanlagringsdiagram för två oberoende
ström-förbrukningar I, och I2; ytan s anger sannolikheten att
samtidigt /, > 5 kA och /, + I, > /s 0=8 k A).
Fig. 4. Samband mellan /,
och s enligt fig. 3.
Fig. 2. Varaktighetsdiagram för strömmen /, i undersökt
ledning och för övrig strömförbrukning /ä inom samma
kraftleverans.
Fig. 1. Varaktighetsdiagram
för strömleverans; Ps
botteneffekt, Wt toppenergi ovan
subtraktionsgräns.
<< prev. page << föreg. sida << >> nästa sida >> next page >>