
Full resolution (JPEG) - On this page / på denna sida - H. 40. 3 november 1953 - Kampekvationer och CTH:s elektriska differentialanalysator, av Henry Wallman, Bo Stjernberg och Erik Elgeskog
<< prev. page << föreg. sida << >> nästa sida >> next page >>
Below is the raw OCR text
from the above scanned image.
Do you see an error? Proofread the page now!
Här nedan syns maskintolkade texten från faksimilbilden ovan.
Ser du något fel? Korrekturläs sidan nu!
This page has never been proofread. / Denna sida har aldrig korrekturlästs.
836
TEKNISK TIDSKRIFT
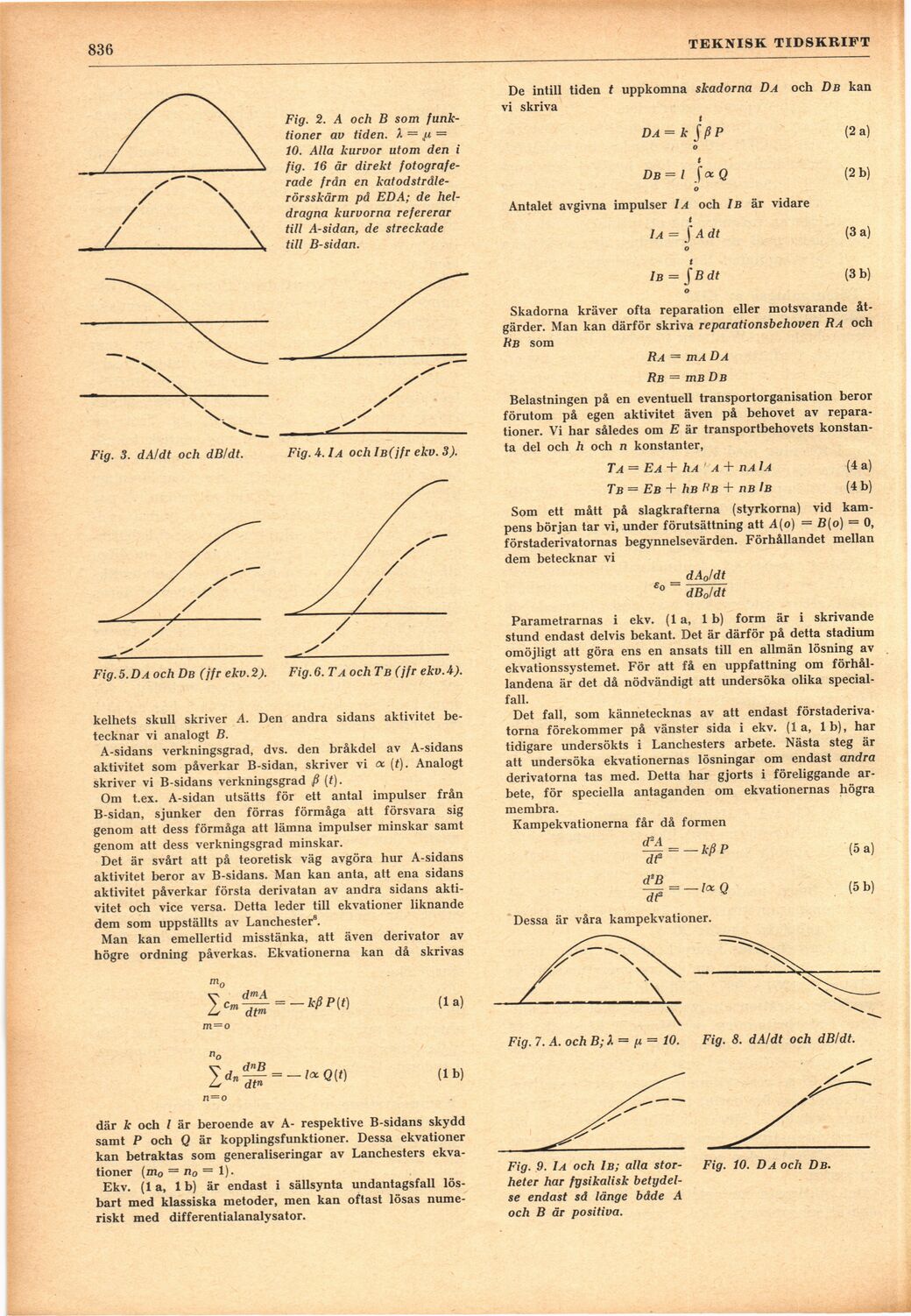
Fig. 2. A och B som
funktioner av tiden. X = jj. =
10. Alla kurvor utom den i
fig. 16 är direkt
fotograferade från en
katodstråle-rörsskärm på EDA; de
heldragna kurvorna refererar
till A-sidan, de streckade
till B-sidan.
Fig. 3. dA/dt och dB! dt. Fig. A. I a och lB(jfr ekv. 3).
Fig. 5.Da och Db (jfr ekv.2). Fig. 6. Ta och Tb (jfr ekv. A).
kelhets skull skriver A. Den andra sidans aktivitet
betecknar vi analogt B.
A-sidans verkningsgrad, dvs. den bråkdel av A-sidans
aktivitet som påverkar B-sidan, skriver vi oc (t). Analogt
skriver vi B-sidans verkningsgrad ß (t).
Om t.ex. A-sidan utsätts för ett antal impulser från
B-sidan, sjunker den förras förmåga att försvara sig
genom att dess förmåga att lämna impulser minskar samt
genom att dess verkningsgrad minskar.
Det är svårt att på teoretisk väg avgöra hur A-sidans
aktivitet beror av B-sidans. Man kan anta, att ena sidans
aktivitet påverkar första derivatan av andra sidans
aktivitet och vice versa. Detta leder till ekvationer liknande
dem som uppställts av Lanchester8.
Man kan emellertid misstänka, att även derivator av
högre ordning påverkas. Ekvationerna kan då skrivas
l
d»B
(la)
(lb)
där k och / är beroende av A- respektive B-sidans skydd
samt P och Q är kopplingsfunktioner. Dessa ekvationer
kan betraktas som generaliseringar av Lanchesters
ekvationer (m0 = n0 = 1).
Ekv. (la, 1 b) är endast i sällsynta undantagsfall
lösbart med klassiska metoder, men kan oftast lösas
numeriskt med differentialanalysator.
De intill tiden t uppkomna skadorna Da och Db kan
vi skriva
t
Da = k § ß P (2 a)
o
t
Db = l f ocq (2 b)
o
Antalet avgivna impulser 1a och Ib är vidare
t
lA = $Adt (3 a)
o
t
lb = $Bdt (3 b)
o
Skadorna kräver ofta reparation eller motsvarande
åtgärder. Man kan därför skriva reparationsbehoven Ra och
Rb som
Ra = mA Da
Rb = mb db
Belastningen på en eventuell transportorganisation beror
förutom på egen aktivitet även på behovet av
reparationer. Vi har således om E är transportbehovets
konstanta del och h och n konstanter,
Ta — Ea + hA ’ A + nA 1a (4 a)
Tb = Eb+ hB ff b + nB Ib (4 b)
Som ett mått på slagkrafterna (styrkorna) vid
kampens början tar vi, under förutsättning att A (o) = B (o) = 0,
förstaderivatornas begynnelsevärden. Förhållandet mellan
dem betecknar vi
= dApldt
e° dB o! dt
Parametrarnas i ekv. (la, 1 b) form är i skrivande
stund endast delvis bekant. Det är därför på detta stadium
omöjligt att göra ens en ansats till en allmän lösning av
ekvationssystemet. För att få en uppfattning om
förhållandena är det då nödvändigt att undersöka olika
specialfall.
Det fall, som kännetecknas av att endast
förstaderiva-torna förekommer på vänster sida i ekv. (la, lb), har
tidigare undersökts i Lanchesters arbete. Nästa steg är
att undersöka ekvationernas lösningar om endast andra
derivatorna tas med. Detta har gjorts i föreliggande
arbete, för speciella antaganden om ekvationernas högra
membra.
Kampekvationerna får då formen
d>B
de
= —l<xQ
(5 a)
(5 b)
Dessa är våra kampekvationer.
Fig. 7. A. och B;X = p = 10. Fig. 8. dA/dt och dB/dt.
Fig. 9. IA och Ib; alla
storheter har fysikalisk
betydelse endast så länge både A
och B är positiva.
Fig. 10. Da och Db.
<< prev. page << föreg. sida << >> nästa sida >> next page >>