
Full resolution (JPEG) - On this page / på denna sida - Nr. 51. 17 december 1915 - Sider ...
<< prev. page << föreg. sida << >> nästa sida >> next page >>
Below is the raw OCR text
from the above scanned image.
Do you see an error? Proofread the page now!
Här nedan syns maskintolkade texten från faksimilbilden ovan.
Ser du något fel? Korrekturläs sidan nu!
This page has never been proofread. / Denna sida har aldrig korrekturlästs.
1 7 december 1915
TEKNISK UKEBLAD
627
/vs. 6
(den tidligere benyttede ordinatakse) som
akse.
Dette vil ikke medføre nogen forandring
i de tidligere fundne
transformationsligninger:
Y____________ A cos a £
A cos (y — o) — sin v £
y____________ A cos (y — a) t]
A cos (y — a) — sin v £
Videre vil vi tænke os ço-planet
paralel-forskjøvet til sammenfald med fotografiet,
eller rettere saa langt at y)-flaten og
fotografiet i virkeligheten blir kongruente. —
Den nye flate — det søkte kart —
para-lel og likedannet den givne flate, vil vi
betegne med Fo og koordinatene for et
punkt i samme med A”o, Yo. — Er videre
x, y koordinatene for det tilsvarende
punkt paa fotografiet, har vi altsaa at
indføre i ovenstaaende ligninger:
X ’ogA= ——
i — j o V — cos a
De nye transformationsligninger
da:
o
t
} o —
t ■ x
cos (y — a)
cos a
cos (y — a)
cos a
blir
(3)
sin vx
y
i
cos (v — a)
––sin vx
cos a
Nævneruttrykket som er det samme i begge
ligninger, fremstiller den rette linje: (L i
fig- 7).
, cos (v — a)
y — — sin v x -j–––––––-t
cos a
Hver enkelt nævner i begge uttryk
fremstilles altsaa grafisk ved ordinaten til
denne linje gjennem det punkt hvis
abscisse er x, lik abscissen for det
betragtede punkt paa fotografiet.
Til bestemmelse av abscissene Ao har
vi altsaa:
eller
Ao: x = t: n,
hvilken proportion gir følgende
konstruktion for de søkte abscisser Ao:
Gjennem punktet p paa fotografiet
trækkes en linje lodret abscisseaksen til
snit med skraalinjen L. Herved er n
bestemt. Fra dette skjæringspunkt
trækkes videre en ret linje gjennem origo.
Denne vil da av linjen y — t avskjære
den søkte abscisse Xo.
Ti
OQ : x — t: n
Betragtes videre et system ordinatlinjer:
To = &
vil de tilsvarende linjer paa
fotografiet hete:
cos (y — «)
/––––->––– y
cos a .
–––––––––––-— b
cos (v — a)
£––-i––-£ — si n v x
cos a
eller ordnet:
(4)
b sin v cos a
t cos (y— a)
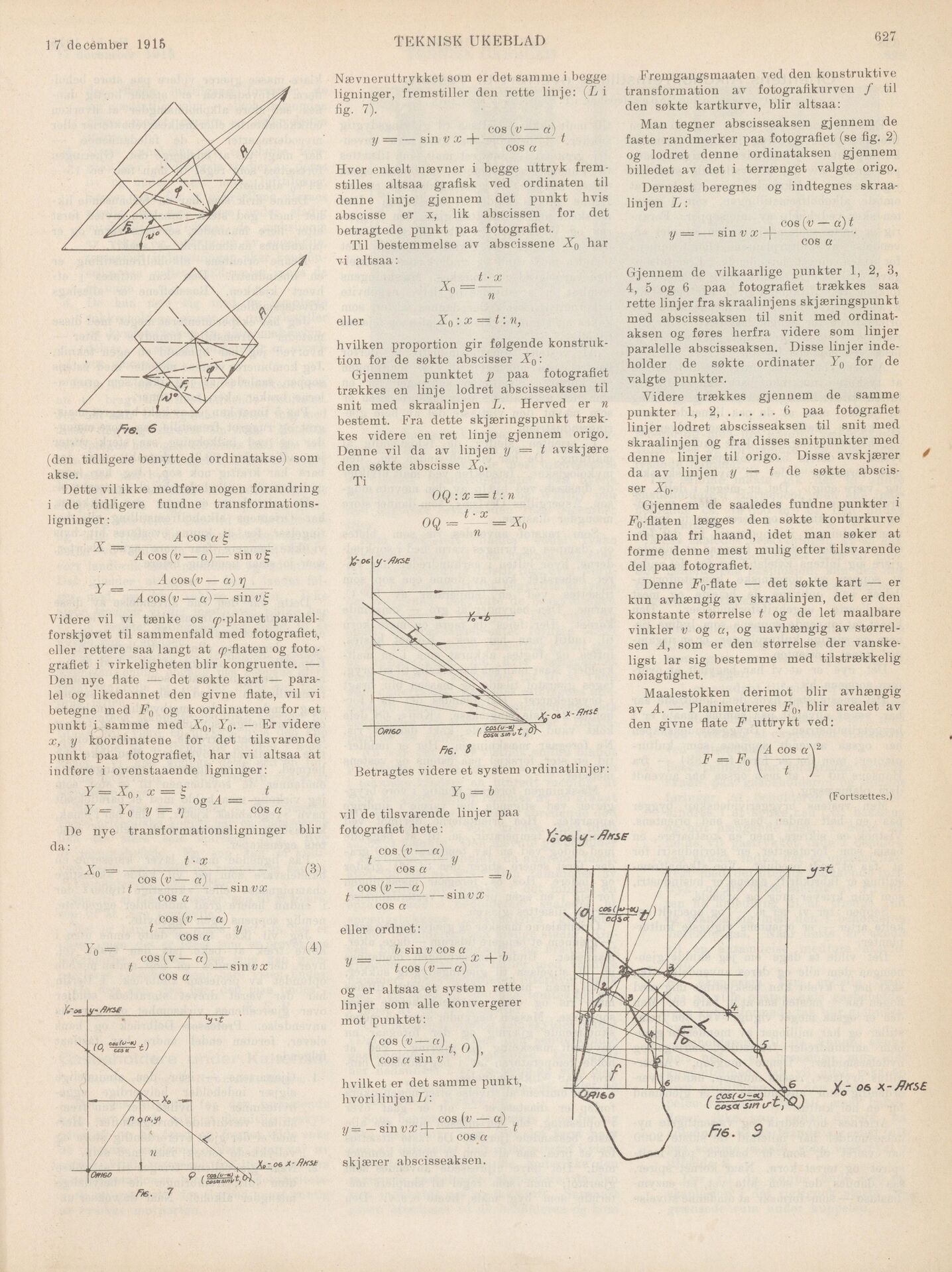
Fremgangsmaaten ved den konstruktive
transformation av fotografikurven / til
den søkte kartkurve, blir altsaa:
Man tegner abscisseaksen gjennem de
faste randmerker paa fotografiet (se fig. 2)
og lodret denne ordinataksen gjennem
billedet av det i terrænget valgte origo.
Dernæst beregnes og indtegnes
skraalinjen L:
cos (y — a) t
y — — sin v x 4––––––––-
cos a
Gjennem de vilkaarlige punkter 1, 2, 3,
4, 5 og 6 paa fotografiet trækkes saa
rette linjer fra skraalinjens skjæringspunkt
med abscisseaksen til snit med
ordinataksen og føres herfra videre som linjer
paralelle abscisseaksen. Disse linjer
indeholder de søkte ordinater Yo for de
valgte punkter.
Videre trækkes gjennem de samme
punkter 1, 2,............6 paa fotografiet
linjer lodret abscisseaksen til snit med.
skraalinjen og fra disses snitpunkter med
denne linjer til origo. Disse avskjærer
da av linjen y — t de søkte
abscisser To.
Gjennem de saaledes fundne punkter i
□Tø-flaten lægges den søkte konturkurve
ind paa fri haand, idet man søker at
forme denne mest mulig efter tilsvarende
del paa fotografiet.
Denne Pø-flate — det søkte kart — er
kun avhængig av skraalinjen, det er den
konstante størrelse t og de let maalbare
vinkler v og a, og uavhængig av
størrelsen A, som er den størrelse der
vanskeligst lar sig bestemme med tilstrækkelig
nøiagtighet.
Maalestokken derimot blir avhængig
av A. — Planimetreres #0, blir arealet av
den givne flate F uttrykt ved:
F Fü
0 \ t )
og er altsaa et system rette
linjer som alle konvergerer
mot punktet:
cos (i; — a)
cos a sin v ’
hvilket er det samme punkt,
hvori linjen L:
, cos (v — a)
y= — sin vx 4—––––––-t
’ cos «
skjærer abscisseaksen.
(Fortsættes.)
<< prev. page << föreg. sida << >> nästa sida >> next page >>