Full resolution (JPEG)
- On this page / på denna sida
- §. 27. Om åtskilligt, som vid jernvägsanläggningar förekommer

<< prev. page << föreg. sida << >> nästa sida >> next page >>
Below is the raw OCR text
from the above scanned image.
Do you see an error? Proofread the page now!
Här nedan syns maskintolkade texten från faksimilbilden ovan.
Ser du något fel? Korrekturläs sidan nu!
This page has been proofread at least once.
(diff)
(history)
Denna sida har korrekturlästs minst en gång.
(skillnad)
(historik)
Vid begagnande af den s. k. Coordinat-methoden förlänger man
vanligen banlinien från den bestämda punkten i rät riktning, och
uppreser sedermera vid vissa punkter uti denna förlängnings-linie,
som utgör tangent till kurven, perpendiklar, hvilka man gör lika
stora med de uträknade afvikelserna från tangenten. Att bestämma
dessa afvikelser enligt någon förminskad scala genom konstruktion,
är likväl hvarken nog tillförlitligt eller altid användbart.
Enklaste formeln för beräkning af coordinaterne till
punkterna uti en båge erhålles enligt följande figur och anvisning.
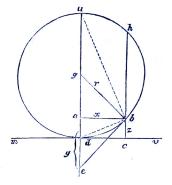
Låt du vara diametern uti cirkeln udbh och dv tangera
cirkeln uti punkten d. Dessa begge linier du och dv kunna nu
betraktas såsom rätvinkliga coordinat-axlar, och alla punkter uti
bågen låta då bestämma sig derigenom, att man söker deras
rätvinkliga afstånd från dessa begge linier. Ty, kalla punktens b
rätvinkliga afstånd från linien dv = z och från du = x, så blifver först
ua : x = x : ad, eller x2 = au . ad; men nu är, om cirkel-radien
sättes = r, ad = z och au = 2r – z, och altså blir x2 = z(2r - z).
Om derföre z vore gifven, så får man lätt värdet af x. Enligt
ofvannämnda æqvation är x2 = z(2r —z), eller
x2 = 2rz - z2
och z2 – 2rz = – x2
z = r +/– qv.-rot(r2 — x2), och får man
således derigenom värdet på z, då x är bekant.
Vore t. ex. en kurvs radie 600’, och man uppreste
perpendiklar på hvar 20:de fots afstånd i den räta banans förlängnings-linie
för att å desamma afsätta kurvens afvikelser från tangenten, så är då
radien eller r = 600’ och x vid första punktens bestämmande = 20’,
vid den andra 40’, vid den tredje 60’ o. s. v., hvarigenom man får
första punkten i kurven, om man insätter dessa värden i
ofvanstående formel: z = r +/– qv.-rot(r2 - x2), som blir z = 600 +/– qv.-rot (6002 — 202),
eller z = 600 +/– qv.-rot(360 000 — 400) = 600 +/– qv.-rot(359 600 = 600 +/– 599,66),
då man således får tvänne värden på z, neml. genom + tecknet 1199,66’,
och genom — tecknet 0,34’, hvilket förra utvisar vinkelräta
afståndet för punkten h från tangenten dv och det sednare punktens
b vinkelräta afstånd från samma tangent, hvilket sistnämnda nu här
användes. På lika sätt erhåller man för den andra punkten,
hvarest z[2] är = 600 ± qv.-rot(6002 — 402), värdena 1198,66’ och 1,34’,
för den tredje 1196,99’ och 3,01’ o. s. v., och bestämmas sålunda
småningom samtliga punkterna i kurven. Vid mycket långa kurver
är likväl denna method hvarken särdeles beqväm eller altid
användbar, hvarföre man i stället tänker sig den punkt, uti hvilken
den räta banlinien tangerar kurven, lagd öfver den på ofvan
angifna sätt sist funna punkten, hvarefter man ånyo afsätter det
redan beräknade kurv-stycket. Härtill fordras likväl, att tangentens
nya riktning i denna punkt bestämmes, hvilket noggrannast sker
derigenom, att man beräknar afskärnings-punkten mellan förra och
nya tangenten, d. v. s., att enligt figuren 50, skulle nu afståndet
df bestämmas.
Emedan gbe är en rät vinkel, så är x2 = ga . ae, och, då
ag är = r — z, så är, om man sätter ae = y, x2 = (r — z)y,
och altså y = x2/(r – z). Nu är vidare de : df = y : x, samt genom
omvexling de : y = df : x; och, emedan de = y — z, så är
(y — z) : y = df : x, eller df = (y – z)x / y. Om man nu deri
substituerar ofvan funna värdet för y, så får man
df = [((x2 / (r – z)) – z) x] / [x2 / (r – z)] = [((x2 / (r — z)) . x) – xz] / [x2 / (r — z)] = x – (z(r — z) / x).
Samma resultat erhålles måhända ännu enklare sålunda:
Utaf de likformiga trianglarne bag och bcf, hvaruti vinklarne
abg och cbf äro lika stora, får man analogien x : ag = bc : cf,
hvaraf följer, då ag = r — z och bc = z, att x : r — z = z : cf, och
[1] Rättelse: Der dv och be skära hvarandra bör stå f.
[2] Rättelse: z i st. f. y
<< prev. page << föreg. sida << >> nästa sida >> next page >>
Project Runeberg, Sun Dec 10 19:43:24 2023
(aronsson)
(diff)
(history)
(download)
<< Previous
Next >>
https://runeberg.org/nivel/0062.html