
Full resolution (JPEG) - On this page / på denna sida - §. 27. Om åtskilligt, som vid jernvägsanläggningar förekommer

<< prev. page << föreg. sida << >> nästa sida >> next page >>
Below is the raw OCR text
from the above scanned image.
Do you see an error? Proofread the page now!
Här nedan syns maskintolkade texten från faksimilbilden ovan.
Ser du något fel? Korrekturläs sidan nu!
This page has been proofread at least once.
(diff)
(history)
Denna sida har korrekturlästs minst en gång.
(skillnad)
(historik)
att cf = z(r — z) / x; samt altså df = x — cf = x – (z(r – z) / x).
Exempelvis må nu antagas, att det vore fråga om att
bestämma läget för tangenten till 10:de punkten i kurven enligt samma
uppgifna dimensioner som förut, så att r = 600’, x (nu i 10:de
punkten) = 200’, då z = 34,32’, hvilka siffervärden man insätter i
den funna formeln för df = x – (z(r — z) / x),
och således df = 200 – (34,32 . (600 — 34,32) / 200) = 102,93’.
I fall, der terrainen ej tillåter några operationer på kurvens
konvexa sida, afsätter man på diametern du stycken efter behag
och beräknar längden på de derifrån i ändpunkterna resta
perpendiklar enligt formeln x2 = z(2r — z), då det är gifvet, att man i
verkligheten ej behöfver uppmäta hela den funna distancen från
diametern ut till bågen, utan med afdrag af den kända distancen
emellan den förra och kordan hc, hvilken korda man då bibehåller
och derifrån vinkelrätt åt höger afsätter de funna skillnaderna.
Oftast förskaffar man sig lättnad uti derefter skeende
byggnadsarbeten, om kurv-punkterna så bestämmas, att de äro till lika
afstånd från hvarandra.
Genom de begge tangenternas gifna riktning är också vinkeln,
under hvilken de skära hvarandra, bestämd. Ty om, enligt fig. 51,
denna vinkel (ABC) sättes = x och bågens radie = r, så blifver
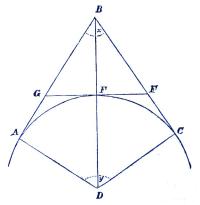 |
| Fig. 51.[1] |
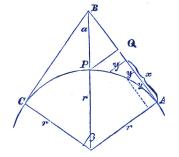 |
| Fig. 52 |
<< prev. page << föreg. sida << >> nästa sida >> next page >>