Handledning uti nivelleringskonsten / 120-121 (1853) Author: Adolf Helander Table of Contents / Innehåll | << Previous | Next >>
	Project Runeberg | Catalog | Recent Changes | Donate | Comments? |

Full resolution (JPEG) - On this page / på denna sida - §. 27. Om åtskilligt, som vid jernvägsanläggningar förekommer

<< prev. page << föreg. sida <<     >> nästa sida >> next page >>

Below is the raw OCR text from the above scanned image. Do you see an error? Proofread the page now!
Här nedan syns maskintolkade texten från faksimilbilden ovan. Ser du något fel? Korrekturläs sidan nu!

This page has been proofread at least once. (diff) (history)
Denna sida har korrekturlästs minst en gång. (skillnad) (historik)

DE lika stora med AB och BC, samt ordinaterna DN och EO lika
stora med BL och CM. Sedermera sammanbindas punkterna D ocb
O, hvarefter OF ocb FG afsättas lika stora med föregående
abscissor, samt FP och GQ lika med ordinaterna, ocb samma operation
förnyas; kunnande man på detta vis fortsätta bågen så långt som
erfordras; och sammanbinder man derefter punkterna A, L, M, N, O
etc., hvarigenom kurvens läge blir bestämdt.

Fig. 58.

Om det ej, såsom i nästföregående method, är fråga om en
cirkelbåge, utan att en kontinuerlig kurv skall afsättas, bestående af
enskilda sådana bågar med samma eller olika stora radier åt olika
sidor om tangenterna, men med kontinuerligt sammanhang
sinsemellan, så kan man då, såsom i nästföregående method, på
tangenterna afsätta lika stora delar eller abscissor, såsom AB och BC,
(fig. 58), med dithörande ordinater. Från midten B af tangenten
AC drages en rät linie till ändpunkten D af ordinaten CD, hvilken
då blir andra tangenten, å hvilken abscissorna DG och GI göras
lika stora med AB och BC, samt ordinaterna FG och HI lika
stora med BE och CD, fastän i omvänd riktning mot dessa, enär
bågen här skall ligga åt motsatt sida. Sedermera fortsätter man,
aldeles såsom i föregående method visas och figuren närmare
upplyser, med iakttagande af radiernas varierande läge, eller, om
ordinaterna skola afsättas ofvanom eller nedanom tangenten, såsom
varande positiva eller negativa. Skulle bågarne vara starkt böjda
måste man använda flera ordinater eller taga kortare abscissor än
eljest; och bör man i öfrigt ihogkomma, att dessa ordinater tagas
hvarandra så nära som behöfligt är, på det kurven måtte få sin
rätta form; äfvensom man måste erinra sig, att kordor och
tangenter i dessa fall altid äro små i jemförelse med radierna. Sist
anförda method gäller äfven i fall, der radierna hafva olika längd, då
tangenterna bestämmas aldeles på samma sätt, endast ordinaterna
sedermera beräknas i förhållande till den förändrade radie-längden.
Vid dessa begge nu anförda methoder är inkel-instrument
obehöfligt, men man måste använda den största noggranhet vid
uppdragande af tangenterna.

För att kunna föra en banlinie genom åtskilliga gifna
punkter fordras i synnerhet att göra ett rigtigt val af radier, för
hvilket ändamål man förut må teckna banlinien i situations-planen och
dervid bestämma desammas storlek, för att sedermera begagna sig
deraf vid utstickning på marken.

Skulle likväl härvid något litet misstag äga rum, så att
radierna ej fullt ut finge den längd de skulle hafva, så har likväl
sådant ej något inflytande på bågens jemna böjning, utan inträffar
endast derigenom, att kurven ej rätt noga kommer att gå genom de
gifna punkterna; men, äfven om denna afvikelse bestiger sig till
flere fot, så har dock detta i praxis ingenting att betyda. Med
någon öfning kan man likväl, under fortsättandet med kurvens
utstickning, lätt välja radier och båglängder så, att man får banan uti en
fortsatt jemn böjning, att gå igenom de bestämda punkterna,
dervid altid ibågkommande, att starka krökningar i möjligaste måtto
undvikas.

Följande uppgifter ifrågakomma vidare att lösa vid
jernban-anläggningar, nemligen:

1:o. Att finna radien, då ett stycke af banbågen i
verkligheten är gifven?

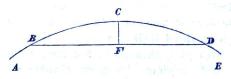Fig. 59.

Drag en korda, BD, och skär densamma midt i tu, samt
genom denna afskärningspunkt F, linien CF vinkelrät mot BD. Sätt
kordan BD = k, höjden CF = h och den sökta radien = r, så blir
r = 4h² + k² / 8h, och bör härvid, för större noggranhets skull,
kordan tagas så stor som möjligt.

Sökes radien till en cirkel, som går genom tre gifna punkter,
så är i allmänhet, om den ena af den genom punkterna gifna
triangelns sida är bekant och sättes = m, samt äfvenså den

<< prev. page << föreg. sida <<     >> nästa sida >> next page >>