Handledning uti nivelleringskonsten / 122-123 (1853) Author: Adolf Helander Table of Contents / Innehåll | << Previous | Next >>
	Project Runeberg | Catalog | Recent Changes | Donate | Comments? |

Full resolution (JPEG) - On this page / på denna sida - §. 27. Om åtskilligt, som vid jernvägsanläggningar förekommer

<< prev. page << föreg. sida <<     >> nästa sida >> next page >>

Below is the raw OCR text from the above scanned image. Do you see an error? Proofread the page now!
Här nedan syns maskintolkade texten från faksimilbilden ovan. Ser du något fel? Korrekturläs sidan nu!

This page has been proofread at least once. (diff) (history)
Denna sida har korrekturlästs minst en gång. (skillnad) (historik)

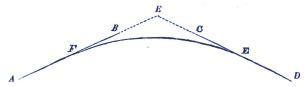
motstående vinkeln = β, radien = r = m / 2 sin. β; ty om, i fig. 56,
radien sökes till en cirkel, som skall gå genom punkterna D, C
och E, så blir, då CD är känd och = m samt vinkeln CED = β,
äfven vinkeln CHD = β och således i triangeln CHD, CD : DH
= sin. β : R, eller m : 2r = sin. β : 1, och altså r = m / (2 sin. β).

2:o. Då tvänne punkter i en båge tillika med radien äro
gifna, att finna tangentens riktning uti endera af dessa
punkter?

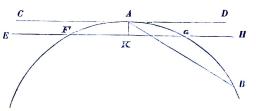Fig. 60.

Punkterna A och B (fig. 60) äro här gifna tillika med
radien. Drag räta limen AB och sök centrivinkeln till halfva denna
korda, såsom förut är visadt (fig. 54), så blir, om samma vinkel
sättes = β sin. β = AB / 2 r. Sätt derefter i A mot AB en
vinkel BAC = 180° — β, så blir AC den åstundade tangenten. Skulle
denna tangent ligga åt motsatta sidan om A, så sättes i samma
punkt mot AB en vinkel BAD = β, då man får tangenten AD.

Finnes bågen på marken afsatt, kan man, äfven utan att
känna radiens längd, uppdraga tangenten sålunda, att man afmäter
tvänne lika stora stycken, AF och AG, från A, och utstakar genom
dessa punkter, F och G, en rät linie, EH, så långt som erfordras,
samt drager sedermera genom A linien CD parallel med EH,
hvilket sednare noggrannast kan ske derigenom, att man utmärker punkter
i den förra på det sätt, att lika stora stycken med AK på ett par
eller flere ställen afsättas vinkelräta från EH.

3:o. Att medelst en cirkelbåge förena tvänne rätliniga
banstycken?

Fig 61.[1]

AB och CD skola här (fig. 61) förenas genom en cirkelbåge.
Bestäm då afskärningspunkten E och vinkeln AED: sätt denna
vinkel = n och radien = r, så blir EF = EH = r /
tang. ¹/₂ n (EH : r
= 1 : tang. ¹/₂ n); och altså, när EH är bekant, blir r = EH (eller
EF) . tang. ¹/₂ n. Är blott ena öfvergångs-punkten F eller H
bestämd, så får man lätt den andra, emedan EF och EH måste vara
lika stora. Skulle punkten E icke vara tillgänglig på fältet, så
kan man på papperet konstruera rätta läget af linierua AB och CD
uti någon stor scala, och såmedelst finna det sökta.

4:o. Om en banbåge är gifven, att då finna
öfvergångs-punkten derå till en rät linie, om meningen är att i sådan
direktion låta banan fortlöpa till någon bestämd punkt?

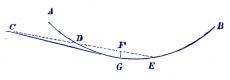Fig. 62.

Låt AB vara den gifna bågen, som skall utlöpa i den gifna
punkten C uti rät linie från en punkt, som då kommer, att utgöra
tangerings-punkten mellan bågen och den tangent, som till
densamma drages från punkten C. Man väljer då en punkt i bågen, t. ex.
E, deråt man förmodar tangerings-punkten ligga. Skulle räta
linien CE då icke skära bågen, utan endast råka den i E, så vore
denna den rätta och sökta punkten. Inträffar åter, såsom här, att
CE skär bågen uti tvänne punkter, så skär DE midt itu uti F och
drag FG vinkelrätt mot DE, så skall G vara den åstundade
tangerings-punkten, som nu sammanbindes med C.

<< prev. page << föreg. sida <<     >> nästa sida >> next page >>