
Full resolution (TIFF) - On this page / på denna sida - Landkort

<< prev. page << föreg. sida << >> nästa sida >> next page >>
Below is the raw OCR text
from the above scanned image.
Do you see an error? Proofread the page now!
Här nedan syns maskintolkade texten från faksimilbilden ovan.
Ser du något fel? Korrekturläs sidan nu!
This page has been proofread at least once.
(diff)
(history)
Denna sida har korrekturlästs minst en gång.
(skillnad)
(historik)
efter som det ene ell. andet Forhold lægges til
Grund, og er derfor ret vilkaarlig. Foruden
efter de 3 foran nævnte Hovedegenskaber (som
areal-, vinkel- og længdetro) kan
Projektionerne saaledes deles efter den Flade, hvorpaa
Punkterne umiddelbart overføres fra Kuglen.
Denne Flade maa enten være selve Planet ell.
en udfoldelig Flade, altsaa Kegle- ell.
Cylinderflade, og man faar derved henh. Azimutal-,
Kegle- eller Cylinderprojektion.
Skønt den første og den sidste egl. kun er
specielle Tilfælde af Kegleprojektionen (Kegle med
Topvinkel henh. 180° og 0°), saa er dog denne
Inddeling ganske praktisk og hyppigt anvendt.
Man taler ogsaa om ægte og uægte Projektion
og forstaar ved de første saadanne, hvor
Punkterne overføres ved rette Linier, udgaaende fra
et bestemt Øjepunkt, medens et saadant ikke
kan tænkes ved de uægte. Endelig kaldes ofte
de Kortprojektioner, hvor Projektionsprincippet
helt er udvisket, vilkaarlige, skønt Punkterne
naturligvis ogsaa her overføres efter en bestemt
Lov. I det flg. skal enkelte af de mest typiske
ell. mest anvendte Kortprojektioner kortelig
omtales.
I. Azimutalprojektioner. En vigtig
Gruppe heraf danner de allerede i Oldtiden
kendte perspektiviske, hvor Billedet af
Jordoverfladen fremstilles paa
Projektionsplanet, som det ses fra et Øjepunkt i
Jorddiameteren til Kortets Midtpunkt (ell. i dennes
Forlængelse). Projektionsplanet tænkes vinkelret
paa denne Diameter, sædvanlig gennem
Jordcentret ell. tangerende Kuglen, men dets Plads
er i øvrigt uden Bet. Derimod er Øjepunktets
Beliggenhed paa Diameteren i mange
Henseender bestemmende for Projektionens Egenskaber,
og 3 Steder er særlig karakteristiske: a) i
Jordoverfladen (modsat Kortets Midtpunkt),
hvorved faas den stereografiske
Projektion, b) i Jordcentret, som giver den
centrale (gnomoniske) Projektion, og c) i
uendelig Afstand, hvorved fremkommer den
ortografiske Projektion. Hver af disse har
igen 3 forsk. Former, efter som Kortets
Midtpunkt falder: 1) i en af Polerne, 2) i et Punkt
af Ækvator, og 3) paa et vilkaarligt Sted
derimellem, og den tilsvarende Form af
Projektionen kaldes henh. Polar-, Ækvatorial-
og Horisontprojektion. I alle disse
Former er Projektionens Hovedegenskaber
selvfølgelig de samme, men Gradnettets
Konstruktion bliver meget forsk., og ved de to
første særlig simpelt.
Den stereografiske Projektion har to
vigtige Egenskaber: den er konform, og enhver
Cirkel paa Jorden fremstilles i Projektion
ogsaa som en Cirkel, der dog i specielle Tilfælde
gaar over til en ret Linie (Cirkel med uendelig
Radius); men i øvrigt giver den betydelige
Forvanskninger i andre Retninger anvendt paa
store Dele af Jorden. Fig. 1 viser Gradnettet
for Halvkuglen i Polarprojektion, hvor alle
Meridianer bliver rette Linier, og Fig. 2 i
Ækvatorialprojektion, hvor dette kun er Tilfældet
med Midtemeridianen og Ækvator. Endelig
viser Fig. 3 Horisontprojektionen, hvor
Konstruktionen er noget mindre simpel. I de
stereografiske Projektioner anvendt paa Halvkuglen
bliver Maalestoksforholdet dobbelt saa stort ved
Randen som i Midten,
Den centrale Projektion, der har samme
3 Former som den foregaaende, anvendes
sjældnere ved L., derimod undertiden til Søkort,
hvor dens specielle Egenskab, at enhver
Storcirkel paa Jorden, altsaa den korteste Vej
mellem to Punkter, fremstilles som en ret Linier
kan være af Bet. I øvrigt medfører
Projektionen store Forvanskninger, idet
Maalestoksforholdet vokser meget stærkt fra Midten til
Banden (for Halvkuglen fra 1 til ∞). Den
ortografiske Projektion har heller ingen
videre Bet. for L., men da den giver samme
Billede som en Kugleoverflade (Globus)
betragtet paa stor Afstand, anvendes den til
Fremstilling af Maanen. I denne Projektion
faar alle Cirkler parallelle med
Projektionsplanet deres rigtige Form og Størrelse; men
Maalestoksforholdet i Retning fra Centrum mod
Banden aftager fra 1 til 0 for Halvkuglen.
Foruden paa de 3 her anførte Steder kan
Øjepunktet tænkes paa ethvert andet Sted af
Jorddiameteren ell. dens Forlængelse, og til
ethvert Sted svarer da en ny Projektion, som
ligger mellem to af de her omtalte uden at
have deres Hovedegenskaber, men som til
Gengæld kan frembyde andre Fordele.
De perspektiviske er »ægte« Projektioner.
Som en stærk Modsætning hertil kan anføres
den meget vilkaarlige
Globularprojektion, der ofte anvendes til Fremstilling af
Jordens Halvkugler (Fig. 4). Ækvator og
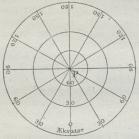 |
| Pig. 1. Stereografisk Polarprojektion. |
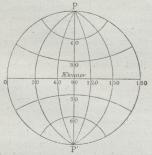 |
| Fig. 2. Stereografisk Ækvatorialprojektion. |
 |
| Fig. 3. Stereografisk Horisontprojektion. |
<< prev. page << föreg. sida << >> nästa sida >> next page >>