
Full resolution (JPEG) - On this page / på denna sida - Sidor ...
<< prev. page << föreg. sida << >> nästa sida >> next page >>
Below is the raw OCR text
from the above scanned image.
Do you see an error? Proofread the page now!
Här nedan syns maskintolkade texten från faksimilbilden ovan.
Ser du något fel? Korrekturläs sidan nu!
This page has never been proofread. / Denna sida har aldrig korrekturlästs.
25 febr. 1928
VÄG- OCH VATTENBYGGNADSKONST
23
Statiskt obestämda system av annan typ eller med
större antal övertaliga storheter behandlas på
fullständigt enahanda sätt, varför ett närmare ingående på
dylika system kan anses onödigt.
Bestämning av influenslinjer för statiskt obestämda system.
I det föregående har redogjorts för tillvägagångssättet
för beräkning av elastiska systems nedböjningslinjer.
Som bekant kunna flertalet problem, som hänföra sig till
bestämmandet av influenslinjer för statiskt obestämda
kvantiteter, omtransformeras till problem, rörande
nedböjningslinjer.
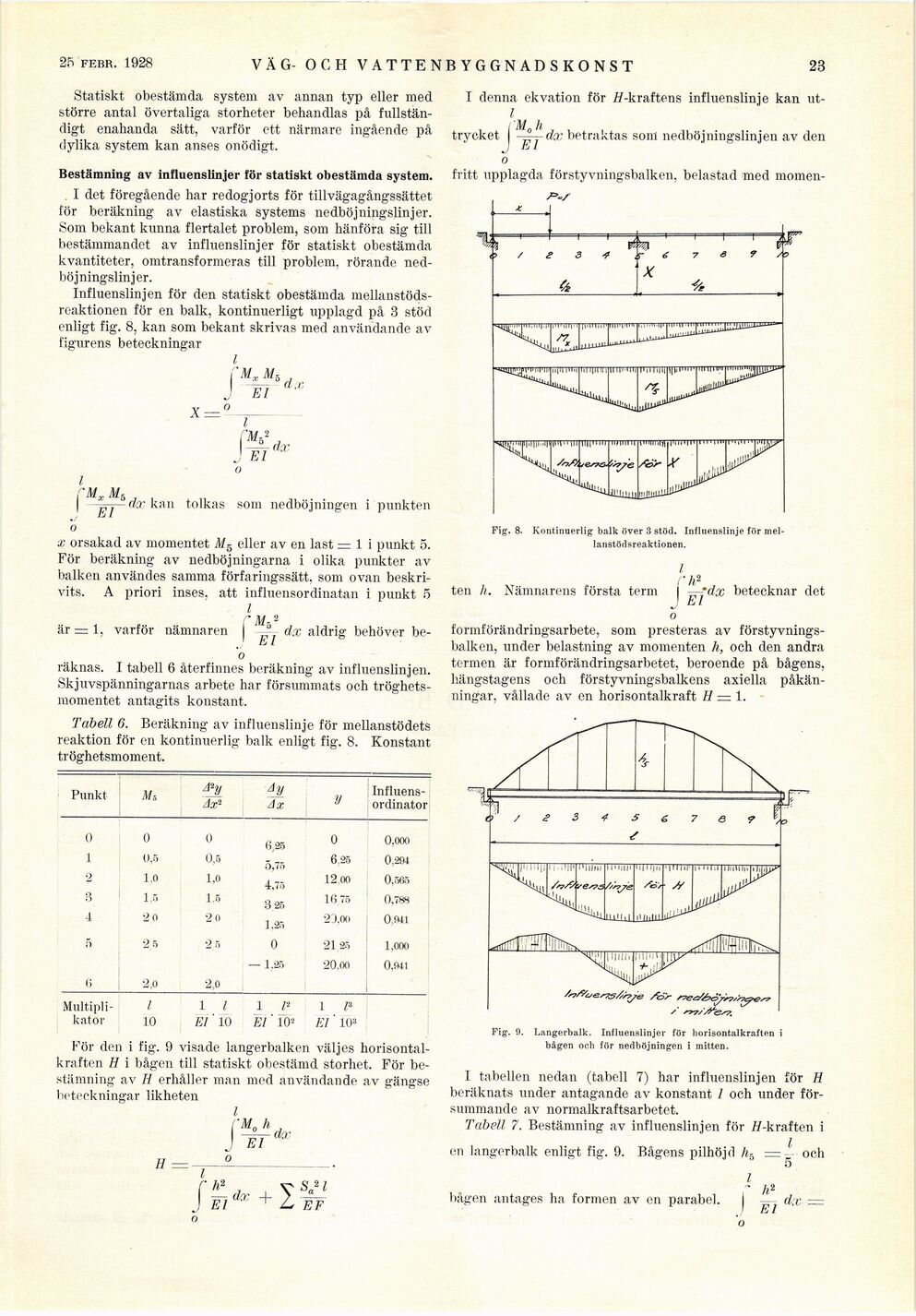
Influenslinjen för den statiskt obestämda
mellanstödsreaktionen för en balk, kontinuerligt upplagd på 3 stöd
enligt fig. 8, kan som bekant skrivas med användande av
figurens beteckningar
l
dx
El
X.
El
dx
[M* Ms
1 El
dx kan tolkas som nedböjningen i punkten
Punkt A*y Ax2 Ay Ax y [-Influens-ordinator-] {+Influens- ordinator+}
0 0 0 6 25 0 0,ooo
1 0,5 0,5 5,75 6 25 0.294
2 1,0 1,0 4,75 12,00 0,565
3 1,5 1.6 3 25 16 75 0,788
4 2 0 2 0 1.25 23,00 0,041
5 2 5 2 5 0 21,25 1.000
— 1,25 20,oo 0,041
6 2,0 2,0
[-Multiplikator-]
{+Multipli- kator+} l 10 1 l El’ 10 1 P El’ 102 1 l3 El’ 103
El
H
h2
El
dx
V s_a
L E
SJl
EF
I denna ekvation för //-kraftens influenslinje kan ut-
l
trycket I ~^~dx betraktas som nedböjningslinjen av den
E l
j
o
fritt upplagda förstyvningsbalken, belastad med momen-
x orsakad av momentet M5 eller av en last = 1 i punkt 5.
För beräkning av nedböjningarna i olika punkter av
balken användes samma förfaringssätt, som ovan
beskrivits. A priori inses, att influensordinatan i punkt 5
l
C M-2
är — 1, varför nämnaren ’’ dx aldrig behöver be-
’ E l
o
räknas. I tabell 6 återfinnes beräkning av influenslinjen.
Skjuvspänningarnas arbete har försummats och
tröghetsmomentet antagits konstant.
Tabell 6. Beräkning av influenslinje för mellanstödets
reaktion för en kontinuerlig balk enligt fig. 8. Konstant
tröghetsmoment.
A/
Fig. 8. Kontinuerlig balk över 3 stöd. Influenslinje för
mel-lanstödsreaktionen.
I
Ch 2
ten h. Nämnarens första term ^rjdx betecknar det
E L
o
formförändringsarbete, som presteras av
förstyvningsbalken, under belastning av momenten h, och den andra
termen är formförändringsarbetet, beroende på bågens,
hängstagens och förstyvningsbalkens axiella
påkänningar, vållade av en horisontalkraft H — 1.
För den i fig. 9 visade langerbalken väljes
horisontalkraften H i bågen till statiskt obestämd storhet. För
bestämning av // erhåller man med användande av gängse
beteckningar likheten
l
f M„ h
- dx
/i/Vueszs/’h/e /£>> ^ea’Sö^/^e^.
Fig. 0. Langerbalk. Influenslinjer för horisontalkraften i
bågen och för nedböjningen i mitten.
I tabellen nedan (tabell 7) har influenslinjen för H
beräknats under antagande av konstant / och under för-
summande av normalkraftsarbetet.
Tabell 7. Bestämning av influenslinjen för //-kraften i
en langerbalk enligt fig. 9. Bågens pilhöjd hr — ’ och
5
l
r h2
bågen antages ha formen av en parabel. i — ■ dx =
’ El
o
<< prev. page << föreg. sida << >> nästa sida >> next page >>