
Full resolution (JPEG) - On this page / på denna sida - Sidor ...
<< prev. page << föreg. sida << >> nästa sida >> next page >>
Below is the raw OCR text
from the above scanned image.
Do you see an error? Proofread the page now!
Här nedan syns maskintolkade texten från faksimilbilden ovan.
Ser du något fel? Korrekturläs sidan nu!
This page has never been proofread. / Denna sida har aldrig korrekturlästs.
21 dec. 1929
SKEPPSBYGGNADSKONST
108
riga stagformerna.
Ävenså kan man
lit-läSci ur figuren att för
de strömlinjeformade
stagen finnes det ett
visst lämpligaste för-
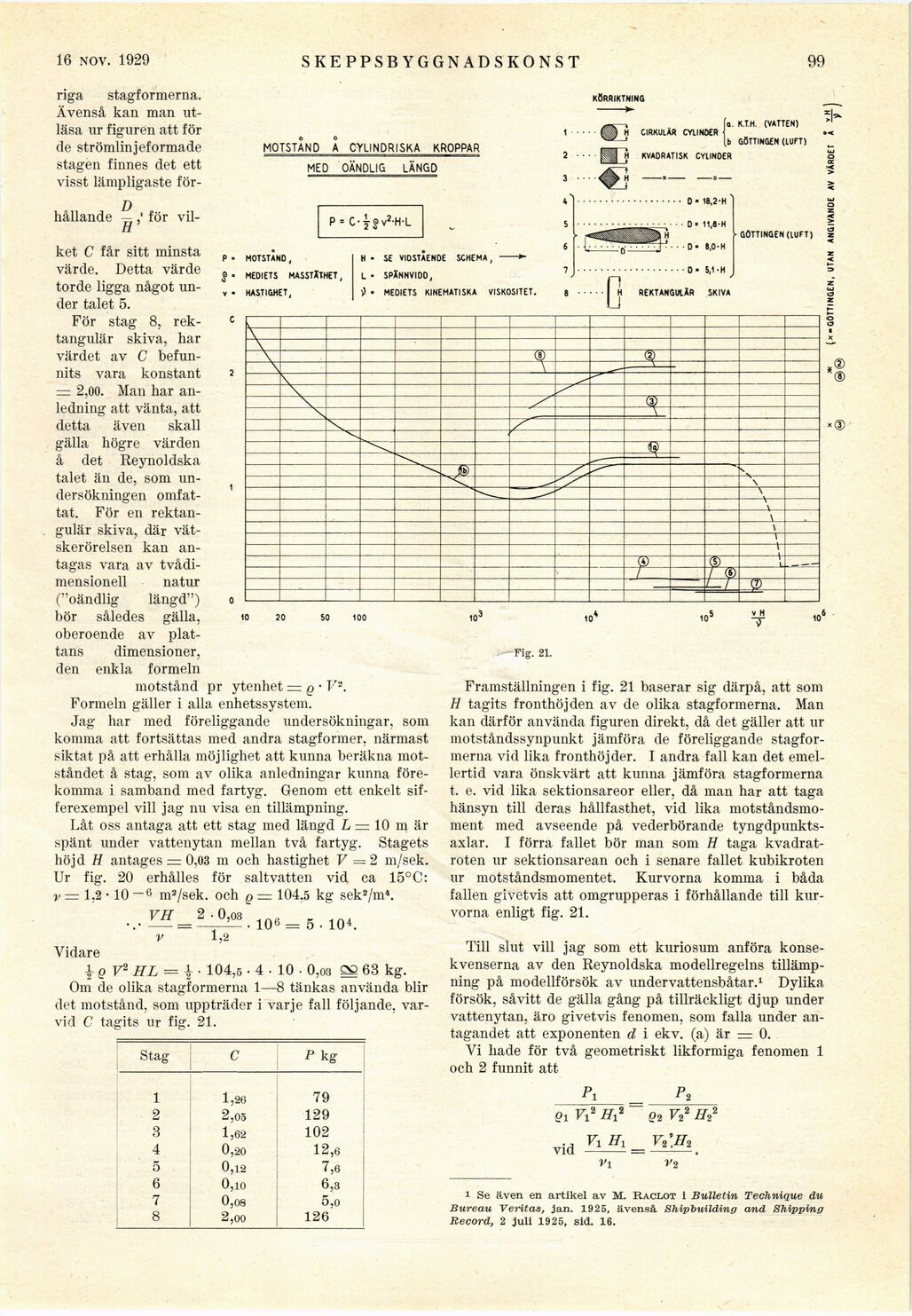
D
H’
KÖRRIKTNING
H CIRKULÄR CYLINDER
MOTSTÅND A CYLINDRISKA KROPPAR
MED OÄNDLIG LÄNGD
K.T.H. (VATTEN)
[b GÖTTINGEN (LUFT)
KVADRATISK CYLINDER
hållande
för vil-
P = C-y<?v2-H-L
MOTSTANO ,
MEDIETS MASSTXTHET,
HASTIGHET,
ket c får sitt minsta
värde. Detta värde
torde ligga något
under talet 5.
För stag 8,
rektangulär skiva, har
värdet av c
befunnits vara konstant
— 2,00. Man har
anledning att vänta, att
detta även skall
gälla högre värden
å det Reynoldska
talet än de, som
undersökningen omfattat. För en
rektangulär skiva, där
vätskerörelsen kan
antagas vara av
tvådimensionell natur
("oändlig längd")
bör således gälla,
oberoende av
plattans dimensioner,
den enkla formeln
motstånd pr ytenhet — g • V3.
Formeln gäller i alla enhetssystem.
Jag har med föreliggande undersökningar, som
komma att fortsättas med andra stagformer, närmast
siktat på att erhålla möjlighet att kunna beräkna
motståndet å stag, som av olika anledningar kunna
förekomma i samband med fartyg. Genom ett enkelt
sifferexempel vill jag nu visa en tillämpning.
Låt oss antaga att ett stag med längd L = 10 m är
spänt under vattenytan mellan två fartyg. Stagets
höjd H antages — 0,03 m och hastighet V — 2 m/sek.
Ur fig. 20 erhålles för saltvatten vid ca 15°C:
v = 1.2 -10-6 m2/sek. och g — 104.5 kg sek2/m4.
io. = b. io*.
V 1,2
Vidare
1 q v2 hl = \ • 104,5 -4-10. 0,03 63 kg.
Om de olika stagformerna 1—8 tänkas använda blir
det motstånd, som uppträder i varje fall följande,
varvid C tagits ur fig. 21.
H - SE VIDSTÅENDE SCHEMA, -*-
L • SPÄNNVIDD,
l) • MEDIETS KINEMATISKA VISKOSITET
0 ■ 18,2-H
11,8-H
8,0-H
0- 5,1 -H
GÖTTINGEN (LUFT)
REKTANGULÄR SKIVA
Stag c p kg
1 1,26 79
2 2,05 129
3 1,62 102
4 0,20 12,6
5 0,12 7,6
6 0,10 6,3
7 0,08 5,0
8 2,oo 126
Fig. 21.
Framställningen i fig. 21 baserar sig därpå, att som
H tagits fronthöjden av de olika stagformerna. Man
kan därför använda figuren direkt, då det gäller att ur
motståndssynpunkt jämföra de föreliggande
stagformerna vid lika fronthöjder. I andra fall kan det
emellertid vara önskvärt att kunna jämföra stagformerna
t. e. vid lika sektionsareor eller, då man har att taga
hänsyn till deras hållfasthet, vid lika
motståndsmoment med avseende på vederbörande
tyngdpunkts-axlar. I förra fallet bör man som H taga
kvadrat-roten ur sektionsarean och i senare fallet kubikroten
ur motståndsmomentet. Kurvorna komma i båda
fallen givetvis att omgrupperas i förhållande till
kurvorna enligt fig. 21.
Till slut vill jag som ett kuriosum anföra
konsekvenserna av den Reynoldska modellregelns
tillämpning på modellförsök av undervattensbåtar.1 Dylika
försök, såvitt de gälla gång på tillräckligt djup under
vattenytan, äro givetvis fenomen, som falla under
antagandet att exponenten d i ekv. (a) är — 0.
Vi hade för två geometriskt likformiga fenomen 1
och 2 funnit att
Pi P2
oi Fi2 HS
Fi Th
vid
q2 v22 h22
v2\h2
vi
v2
i Se även en artikel av M. Raclot i Bulletin Technique du
Bureau Veritas, jan. 1925, ävenså Shipbuilding and Shippmg
Record, 2 juli 1925, sid. 16.
<< prev. page << föreg. sida << >> nästa sida >> next page >>