
Full resolution (JPEG) - On this page / på denna sida - Sidor ...
<< prev. page << föreg. sida << >> nästa sida >> next page >>
Below is the raw OCR text
from the above scanned image.
Do you see an error? Proofread the page now!
Här nedan syns maskintolkade texten från faksimilbilden ovan.
Ser du något fel? Korrekturläs sidan nu!
This page has never been proofread. / Denna sida har aldrig korrekturlästs.
108
TEKNISK TIDSKRIFT
20 SePt. 1930
9-
’V
Si
l
sin ßt +
v
*1=7
Första derivatan av parentesen är
24
sin n ßt
9-
l 3
- ß eos ßt -f -
V
Gi
-l— 1
8
och då eos 3 ßt = 4 eos3
för bestämning av den
uppstår
1
-ß eos 3 ßt
ßt~
tid,
- 3 eos ßt, erhåller man
efter vilken maximum
arc sm
WI
(74)
l—l
Insattes detta värde i ovanstående formel för s1 och
beaktar man, att sin3 ßt = 3 sin ßt — 4 sin3 ßt, så
erhålles för bromsvägen en funktion som lyder
3 C/a’1 k
•’imai —
Av ekv. (31) framgår, att — l, för ifrågavarande fall
Gi
erhåller storleken
k ,100
Gi ~ 18 ’
1
’Gi
{Gi ’ 324 9 \Gi
och insattes i enlighet med vad som ovan påvisats de
värden, som motsvara -{-tecknet framför rotmärket, så
erhåller slmax följande storlek
0,736 ■ V\J l
i
24 — 6
. Ö2
+ 3\/’
64 — 36
G»
(76)
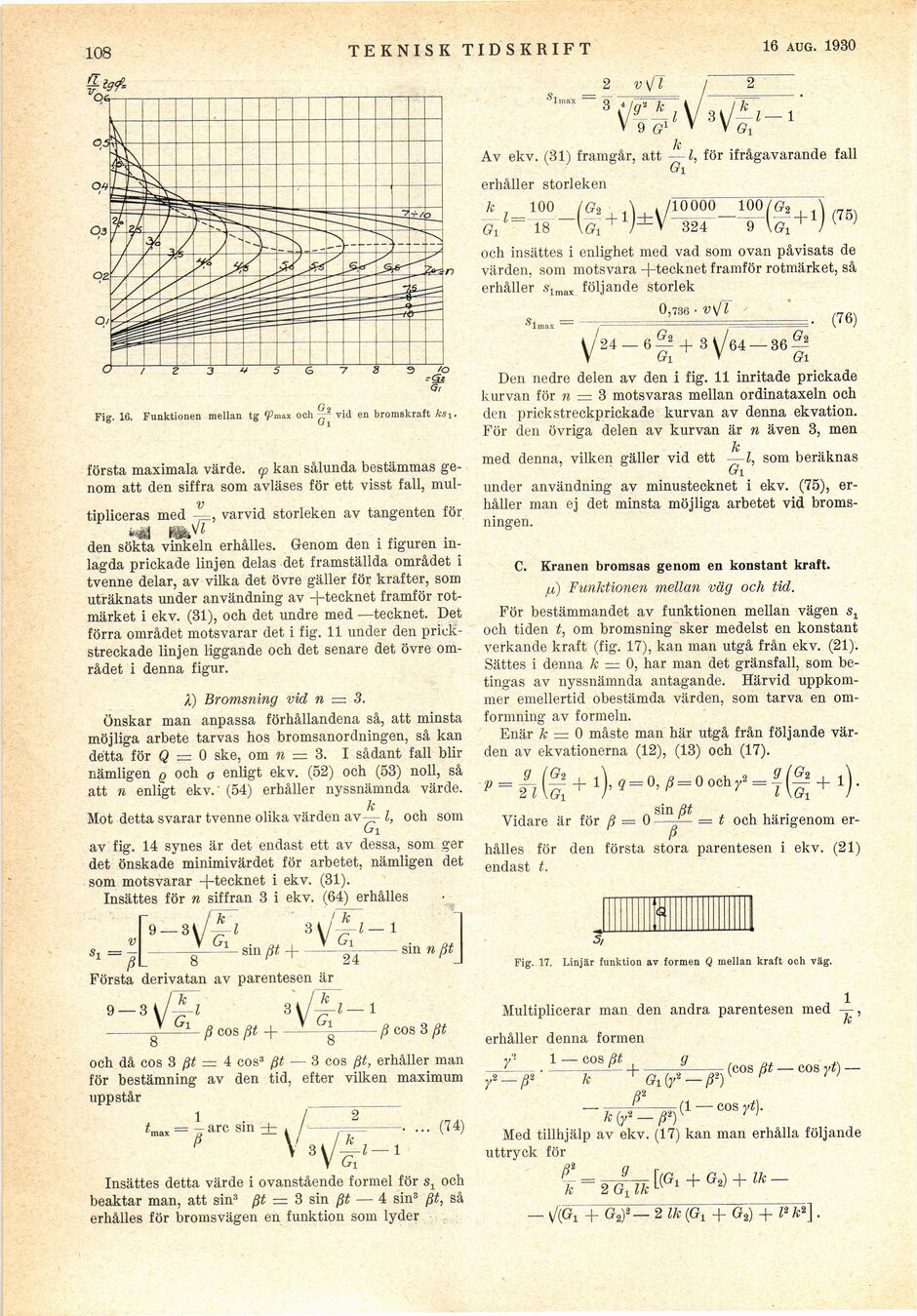
Fig. 16. Funktionen mellan tg ^Pmax och vid en bromskraft ks i.
"i
första maximala värde, (p kan sålunda bestämmas
genom att den siffra som avläses för ett visst fall,
inulls
tipliceras med —, varvid storleken av tangenten för
Nä mA
den sökta vinkeln erhålles. Genom den i figuren
inlagda prickade linjen delas det framställda området i
tvenne delar, av vilka det övre gäller för krafter, som
uträknats under användning av -{-tecknet framför
rotmärket i ekv. (31), och det undre med —tecknet. Det
förra området motsvarar det i fig. 11 under den
prick-streckade linjen liggande och det senare det övre
området i denna figur.
X) Bromsning vid n — 3.
önskar man anpassa förhållandena så, att minsta
möjliga arbete tarvas hos bromsanordningen, så kan
detta för Q — 0 ske, om n — 3. I sådant fall blir
nämligen q och o enligt ekv. (52) och (53) noll, så
att n enligt ekv. (54) erhåller nyssnämnda värde.
k
Mot detta svarar tvenne olika värden av — l, och som
Gi
av fig. 14 synes är det endast ett av dessa, som ger
det önskade minimivärdet för arbetet, nämligen det
som motsvarar -{-tecknet i ekv. (31).
Insattes för n siffran 3 i ekv. (64) erhålles
k . „ . / k
V Gl ■ V Gl
Den nedre delen av den i fig. 11 inritade prickade
kurvan för n — 3 motsvaras mellan ordinataxeln och
den prickstreckprickade kurvan av denna ekvation.
För den övriga delen av kurvan är n även 3, men
k
med denna, vilken gäller vid ett —l, som beräknas
öi
under användning av minustecknet i ekv. (75),
erhåller man ej det minsta möjliga arbetet vid
bromsningen.
C. Kranen bromsas genom en konstant kraft.
ju) Funktionen mellan väg och tid.
För bestämmandet av funktionen mellan vägen s±
och tiden t, om bromsning sker medelst en konstant
verkande kraft (fig. 17), kan man utgå från ekv. (21).
Sättes i denna k — 0, har man det gränsfall, som
betingas av nyssnämnda antagande. Härvid
uppkommer emellertid obestämda värden, som tarva en
omformning av formeln.
Enär k = 0 måste man här utgå från följande
värden av ekvationerna (12), (13) och (17).
g (Os
= 0 och
= 9(G»
I Vßi
+ 1
Vidare är för ß — 0 Sm ^ = t och härigenom er-
ß
hålles för den första stora parentesen i ekv. (21)
endast t.
Fig. 17. Linjär funktion av formen Q mellan kraft och väg.
Multiplicerar man den andra parentesen med —
1
T
erhåller denna formen
y’! 1 — eos ßt
k
Gi(f-ß2)
(eos ßt — eos yt) ■
ß’1
- (1 — eos yt).
k(f-ß*y
Med tillhjälp av ekv. (17) kan man erhålla följande
uttryck för
— \f(Oi + Gif— 2 Ik (Gi + Gi) + P Ä9] .
<< prev. page << föreg. sida << >> nästa sida >> next page >>