
Full resolution (TIFF) - On this page / på denna sida - Sidor ...
<< prev. page << föreg. sida << >> nästa sida >> next page >>
Below is the raw OCR text
from the above scanned image.
Do you see an error? Proofread the page now!
Här nedan syns maskintolkade texten från faksimilbilden ovan.
Ser du något fel? Korrekturläs sidan nu!
This page has never been proofread. / Denna sida har aldrig korrekturlästs.
36
TEKNISK TIDSKRIFT
16 MAJ 1931
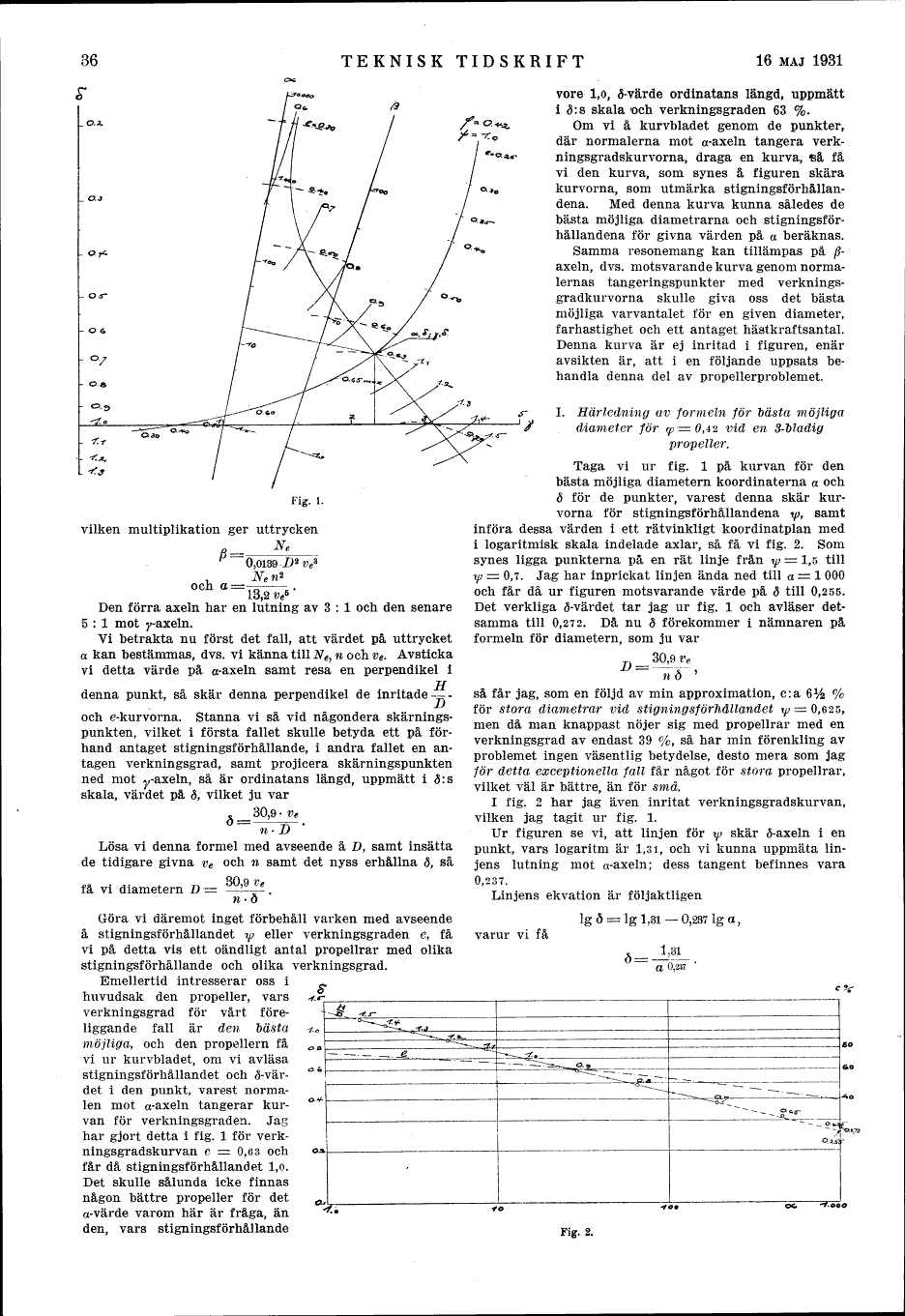
Fig. 1.
vilken multiplikation ger uttrycken
0,0139 D2 Ve*
ocha-Nen2
°Clia-T3^-
Den förra axeln har en lutning av 3 : l och den senare
5 : l mot y-axeln.
Vi betrakta nu först det fall, att värdet på uttrycket
a kan bestämmas, dvs. vi känna till Ne, n och ve. Avsticka
vi detta värde på a-axeln samt resa en perpendikel i
[-T/denna-]
{+T/-
denna+} punkt, så skär denna perpendikel de inritade -
och e-kurvorna. Stanna vi så vid någondera
skärningspunkten, vilket i första fallet skulle betyda ett på
förhand antaget stigningsförhållande, i andra fallet en
antagen verkningsgrad, samt projicera skärningspunkten
ned mot y-axeln, så är ordinatans längd, uppmätt i 6:s
skala, värdet på d, vilket ju var
v_30,9’ ve
~~~~n~> D
Lösa vi denna formel med avseende å D, samt insätta
de tidigare givna ve och n samt det nyss erhållna d, så
få vi diametern D = – Ve.
n - ö
Göra vi däremot inget förbehåll varken med avseende
å stigningsförhållandet y> eller verkningsgraden e, få
vi på detta vis ett oändligt an
stigningsförhållande och olika
Emellertid intresserar oss i
huvudsak den propeller, vars
verkningsgrad för vårt
föreliggande fall är den lästa
möjliga, och den propellern få
vi ur kurvbladet, om vi avläsa
stigningsförhållandet och
6-vär-det i den punkt, varest
normalen mot a-axeln tangerar
kurvan för verkningsgraden. Jag
har gjort detta i fig. l för
verkningsgradskurvan e = 0,63 och
får då stigningsförhållandet l,o.
Det skulle sålunda icke finnas
någon bättre propeller för det
a-värde varom här är fråga, än
den, vars stigningsförhållande
vore l,o, 6-värde ordinatans längd, uppmätt
i 6:s skala och verkningsgraden 63 %.
Om vi å kurvbladet genom de punkter,
där normalerna mot a-axeln tangera
verkningsgradskurvorna, draga en kurva, så få
vi den kurva, som synes å figuren skära
kurvorna, som utmärka
stigningsförhållandena. Med denna kurva kunna således de
bästa möjliga diametrarna och
stigningsförhållandena för givna värden på a beräknas.
Samma resonemang kan tillämpas på
/?-axeln, dvs. motsvarande kurva genom
norma-lernas tangeringspunkter med
verkningsgradkurvorna skulle giva oss det bästa
möjliga varvantalet för en given diameter,
farhastighet och ett antaget hästkraftsantal.
Denna kurva är ej inritad i figuren, enär
avsikten är, att i en följande uppsats
behandla denna del av propellerproblemet.
I. Härledning av formeln för bästa möjliga
diameter -för (p-0,42 vid en 3-~bladig
propeller.
Taga vi ur fig. l på kurvan för den
bästa möjliga diametern koordinaterna a och
ö för de punkter, varest denna skär
kurvorna för stigningsförhållandena */;, samt
införa dessa värden i ett rätvinkligt koordinatplan med
i logaritmisk skala indelade axlar, så få vi fig. 2. Som
synes ligga punkterna på en rät linje från ip - 1,5 till
yj = 0,7. Jag har inprickat linjen ända ned till a - l 000
och får då ur figuren motsvarande värde på d till 0,255.
Det verkliga 6-värdet tar jag ur fig. l och avläser
detsamma till 0,272. Då nu d förekommer i nämnaren på
formeln för diametern, som ju var
__ 30,9 ve
w ö""’
så får jag, som en följd av min approximation, c:a G1/^ %
för stora diametrar vid stigning s förhållandet y = 0,625,
men då man knappast nöjer sig med propellrar med en
verkningsgrad av endast 39 %, så har min förenkling av
problemet ingen väsentlig betydelse, desto mera som jag
för detta exceptionella fall får något för stora propellrar,
vilket väl är bättre, än för små.
I fig. 2 har jag även inritat verkningsgradskurvan,
vilken jag tagit ur fig. 1.
Ur figuren se vi, att linjen för \p skär 6-axeln i en
punkt, vars logaritm är l,si, och vi kunna uppmäta
linjens lutning mot a-axeln; dess tangent befinnes vara
0,237.
Linjens ekvation är följaktligen
varur vi få
Ig ö = Ig 1,81 - 0,237 Ig a,
i Pl
rkr S
0 & 0 (»
&..¥. O.A
c?./
^opellrar med olika 1.31 lingsgrad. " = "TTö^T ’
^ ^
*~-~^£+^ ^j
~c^~~~~-^-^^ ~r. «_
°^~~^- -7 f
–––––– – JL ^
–^–T:,,
- . - ..
- . -^^r^^^^o. 9
~~"^~-~_ O^A ~~
, _____
^__ ^’~~~ ~~ -. ____ __
^^^–^J"-
Q«
Fig. 2.
<< prev. page << föreg. sida << >> nästa sida >> next page >>