
Full resolution (TIFF) - On this page / på denna sida - Sidor ...
<< prev. page << föreg. sida << >> nästa sida >> next page >>
Below is the raw OCR text
from the above scanned image.
Do you see an error? Proofread the page now!
Här nedan syns maskintolkade texten från faksimilbilden ovan.
Ser du något fel? Korrekturläs sidan nu!
This page has never been proofread. / Denna sida har aldrig korrekturlästs.
24 OKT. 1931
VÄG- OCH VATTENBYGGNADSKONST
137
Tab.
-+J
i
i
i
i i
^4
pH
S
y
h
y1 v’2
IV2
(l + 2/’2)3/2
V}ant
-".’T
h
y\ W°’~ti\
-»’T
T-T
^’
r,’
r\
w . a
V ber
-*lo -f 1
«.fi
"
0
20
400
1,400
L,66
0
0
0
0
0
0
a
0 a.
0
0
0
0
’
19
18
324
1,324
1,52
3
1,9
4,9 ;
1
4
-T,
a- 7,5
1
30
30
16,o
46,0
2
36
16
256
1,256
1,41
5
3,6
8,6
2
7
-12,1
a- 19,6
2- 7,5
60
52,5
32,o
84,5
3
51
14
196
1,196
i, 31
5
5,1
10,1 |
i
3
8
-13,2
a- 32,8
3- 27,1
90
62,9
48,0
110,9
4
64
12
144
1,144
1,23
4
6,4
10,4
4
8
- 12,8
a- 45,6
4- 59,9
120
60,1
64,o
124,1
5
75
10
100
1,100
1,16
2
7,5
9,5
5
7
-11,0
a-56,6
5-105,5
150
44,5
80,0
124,5
i
6
84
8
64
1,064
J, 10
0
8,4
8,4
6
6
- 9,2
a- 65,8
6-162,1
180
17,9
96,1
114,0
7
91
6
36
1,036
1,05
- 2
9,1
7,1 ;
7
5
- 7,5
a- 73,3
7-227,9
210
- 17,9
112,1
94,2
i
8
96
4
16
1,016
1,02
- 5
9,6
4,6
8
3
~ 4,7
a- 78,0
8-301,2
240
- 61,2
128,1
66,9
9
99
2
4
1,004
1,005
__ 7
.
9,9
2,9
9
2
- 2,9
a- 80,9
9-379,2
270
-109,2
144,1
34,9
i 10
100
0
o
1,000
1,000
-10
10,0
0
10
0
0
10-460.1
300
-160,1
160,1
o !
1
löö
h 10 1
lk}2
Vio//
1
1
i
H El
H 1 El’ 10
Ä.(M2 E i \io;
H ll]2 £7’vLO/
H ll\2 £/’W
H i M2
W! ’ \io/
n /zv2
EI’\IQ]
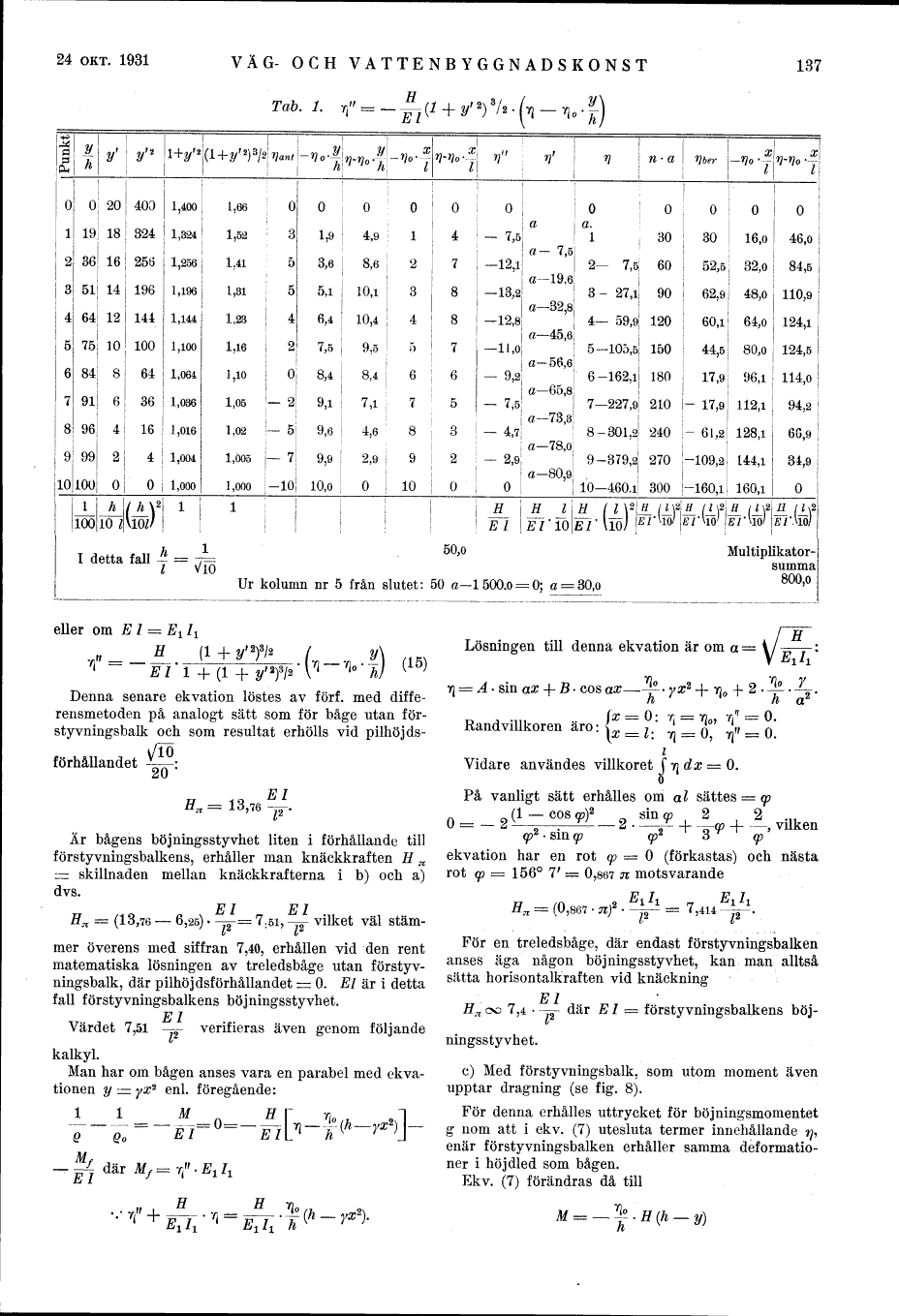
I detta fall - = 7= Z v/io
50,0
Multiplikator-summa 800 o
Ur kolumn nr 5 från slutet: 50 a- 1500.0 = 0; a = 30,0
OvA/jV
y
-^- (15)
eller om E I =
H
Denna senare ekvation löstes av förf. med
differensmetoden på analogt sätt som för båge utan
för-styvningsbalk och som resultat erhölls vid
pilhöjds-förhållandet
20 ’
Är bågens böjningsstyvhet liten i förhållande till
förstyvningsbalkens, erhåller man knäckkraften H n
n= skillnaden mellan knäckkrafterna i b) och a)
dvs.
; - 6,25) .
El
= 7,5i,-yö-vilket väl stäm-
mer överens med siffran 7,40, erhållen vid den rent
matematiska lösningen av treledsbåge utan
förstyv-ningsbalk, där pilhöjdsförhållandet = 0. El är i detta
fall förstyvningsbalkens böjningsstyvhet.
El
Värdet 7,51 -^ verifieras även genom följande
L
kalkyl.
Man har om bågen anses vara en parabel med
ekvationen y~yx* enl. föregående:
Ä ~
Mf A~ M
- -^ dar Mf =
l ff
Lösningen till denna ekvation är om a = V/TTT~:
V "i*i
ri = A.$max-{-B. cosax–/~7#2+ vj0 + 2 .-£..-£..
/^ ti ÖL
(x - O ’ T = Y) T/’ -^ O
Randvillkoren äro: { 7." J! _ o ’ Jw - o’
JjE = f,. A] - U, 7] - U.
l
Vidare användes villkoret (väx-Q.
o
På vanligt sätt erhålles om al sättes = cp
. (l - cos «>)2 sin o? 2 2 ."
O = _ 2V . ry––-2 . -/ + -9? H–––, vilken
9?2 . sm <p <^?2 3 T (p
ekvation har en rot cp = O (förkastas) och nästa
rot cp = 156° 7’ = 0,867 JT motsvarande
U /A ,2 ^1 ^1 rr ^1 ^1
^ - (0,867 - JZJ2 - -p- - 7,414 -p-.
För en treledsbåge, där endast förstyvningsbalken
anses äga någon böjningsstyvhet, kan man alltså
sätta horisontalkraften vid knackning
F1 J
Ha co 7,4 . -jg- där # 7 = förstyvningsbalkens
böj-L
ningsstyvhet.
c) Med förstyvningsbalk, som utom moment även
upptar dragning (se fig. 8).
För denna erhålles uttrycket för böjningsmomentet
g nom att i ekv. (7) utesluta termer innehållande 77,
enär förstyvningsbalken erhåller samma
deformationer i höjdled som bågen.
Ekv. (7) förändras då till
<< prev. page << föreg. sida << >> nästa sida >> next page >>