
Full resolution (TIFF) - On this page / på denna sida - Häfte 1. Jan. 1933 - Vidar Ekström: Beräkning medelst nomogram av energiförlusterna i en elektrisk kraftöverföring
<< prev. page << föreg. sida << >> nästa sida >> next page >>
Below is the raw OCR text
from the above scanned image.
Do you see an error? Proofread the page now!
Här nedan syns maskintolkade texten från faksimilbilden ovan.
Ser du något fel? Korrekturläs sidan nu!
This page has never been proofread. / Denna sida har aldrig korrekturlästs.
10
TEKNISK TIDSKRIFT
7 JAN. 1933
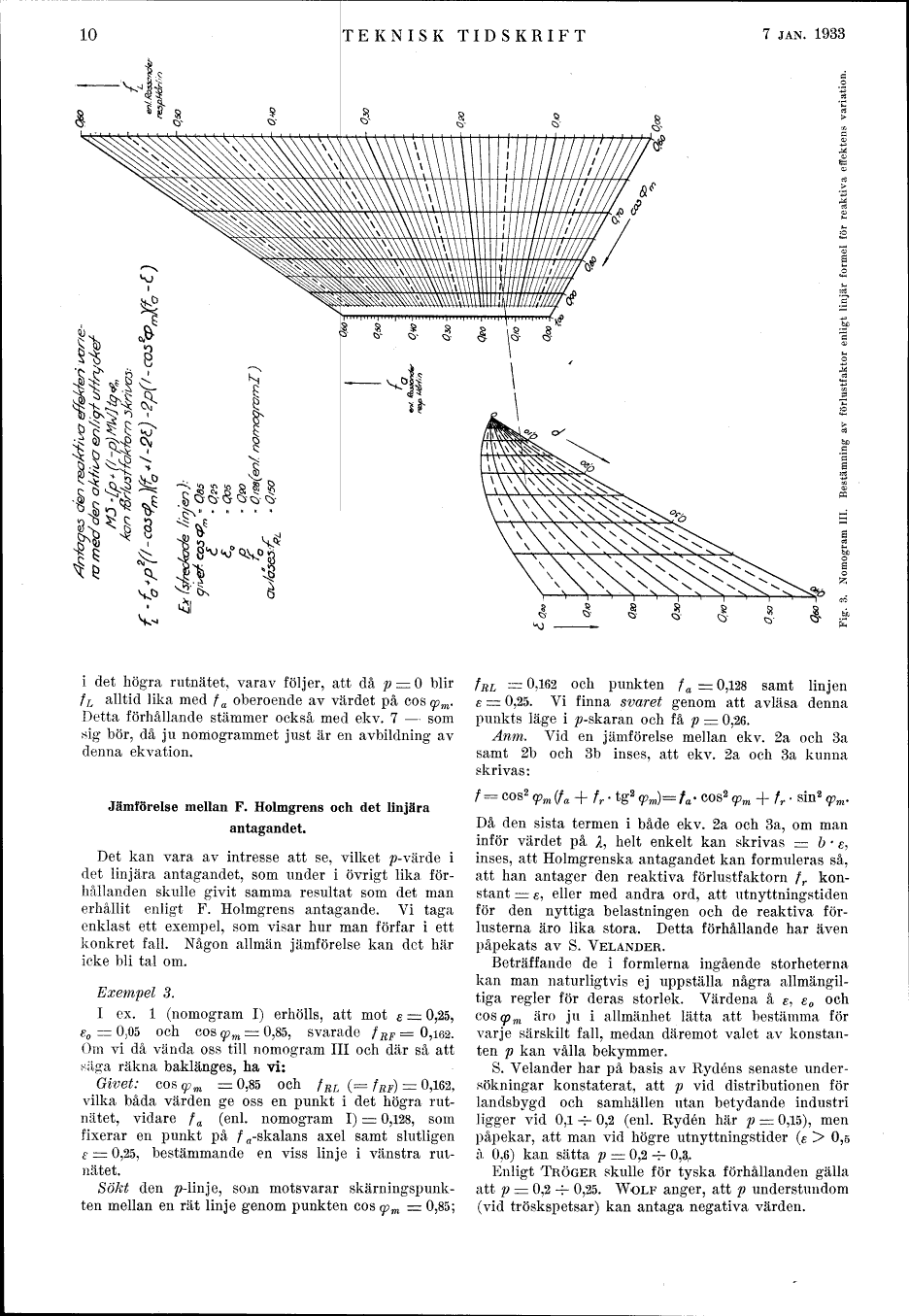
Fig-. 3. Nomogram III. Bestämning av förlustfaktor enligt linjär formel för re aktiva effektens variation.
i åvt högra rutnätet, varav följer, att då p = O blir
fL alltid lika med fa oberoende av värdet på cos q>m.
Detta förhållande stämmer också med ekv. 7 - som
sig bör, då ju nomogrammet just är en avbildning av
denna ekvation.
Jämförelse mellan F. Holmgrens och det linjära
antagandet.
Det kan vara av intresse att se, vilket p-värde i
det linjära antagandet, som under i övrigt lika
förhållanden skulle givit samma resultat som det man
erhållit enligt F. Holmgrens antagande. Vi taga
enklast ett exempel, som visar hur man förfar i ett
konkret fall. Någon allmän jämförelse kan det här
icke bli tal om.
Exempel 3.
I ex. l (nomogram I) erhölls, att mot s - 0,25,
s0 = 0;05 och cos (pm - 0,85, svarade /BF=0,i62.
Om vi då vända oss till nomogram III och där så att
säga räkna baklänges, ha vi:
Givet: cos <pm = 0,85 och fRL (= fRF) - 0,162,
vilka båda värden ge oss en punkt i det högra
rutnätet, vidare fa (enl. nomogram I) = 0,128, som
fixerar en punkt på fa-skalans axel samt slutligen
£ - 0,25, bestämmande en viss linje i vänstra
rutnätet.
Sökt den p-linje, som motsvarar
skärningspunkten mellan en rät linje genom punkten cos ym = 0,85;
fRL :=0,162 och punkten fa - 0,128 samt linjen
e = 0,25. Vi finna svaret genom att avläsa denna
punkts läge i ^-skaran och f å p - 0,26.
Anm. Vid en jämförelse mellan ekv. 2a och 3a
samt 2b och 3b inses, att ekv. 2a och 3a kunna
skrivas:
= cos
(fa + fr . tg2 (pm)= fa- cos2
sin2 q>
Då den sista termen i både ekv. 2a och 3a, om man
inför värdet på h helt enkelt kan skrivas - b - £,
inses, att Holmgrenska antagandet kan formuleras så,
att han antager den reaktiva f örlustf aktorn fr
konstant - g, eller med andra ord, att utnyttningstiden
för den nyttiga belastningen och de reaktiva
förlusterna äro lika stora. Detta förhållande har även
påpekats av S. VELANDER.
Beträffande de i formlerna ingående storheterna
kan man naturligtvis ej uppställa några
allmängiltiga regler för deras storlek. Värdena å £, e0 och
Cos9?m äro ju i allmänhet lätta att bestämma för
varje särskilt fall, medan däremot valet av
konstanten p kan vålla bekymmer.
S. Velander har på basis av Rydéns senaste
undersökningar konstaterat, att p vid distributionen för
landsbygd och samhällen utan betydande industri
ligger vid 0,1 -f- 0,2 (enl. Rydén här p - 0,15), men
påpekar, att man vid högre utnyttningstider (s > 0,5
å 0,6) kan sätta p = 0,2 -f- 0,3,
Enligt TRÖGER skulle för tyska förhållanden gälla
att p = 0,2 -^ 0,25. WOLF anger, att p understundom
(vid tröskspetsar) kan antaga negativa värden.
<< prev. page << föreg. sida << >> nästa sida >> next page >>