
Full resolution (JPEG) - On this page / på denna sida - Sidor ...
<< prev. page << föreg. sida << >> nästa sida >> next page >>
Below is the raw OCR text
from the above scanned image.
Do you see an error? Proofread the page now!
Här nedan syns maskintolkade texten från faksimilbilden ovan.
Ser du något fel? Korrekturläs sidan nu!
This page has never been proofread. / Denna sida har aldrig korrekturlästs.
Mekanik.
parabelskaran på en ellips med ena halvaxeln =
1 u2
och andra halvaxeln — -— A.
2 2 g
Efter y-axeln se vi förutom fa även c2, och efter
Även v)2 kan erhållas ur dia-
æ-axeln står ju wa.
grammet, ty är ju
w9 —
Wg
sin y
varför lätt kurvor för konstanta värden å w2 kunna
uppritas. I diagrammet är sålunda en kurva för
w.2 — 380 m/sek. inritad, och berör denna även
enveloppen.
I. Avloppsförlusten vid vanliga för-
hållanden.
Under vanliga förhållanden brukar det ej finnas
någon anledning till att strålens avgångsvinkel y är
avvikande från skovelns avloppsvinkel ß, ty vid
hastigheter lägre än ljudhastigheten känner, så att
säga, den framströmmande ångströmmen vilket
tryckförhållande, som råder vid avloppet, och inställer sig
tryckförloppet så, att, även om avloppstillståndet är
helt annat än det, för vilket löphjulet konstruerats,
ångstrålen utfyller och följer skovelkanalen.
Vid lägre hastigheten å w,2 än ljudhastigheten kan
sålunda †a direkt tagas ur kurvan i diagram fig. 1
och avläsas vid kurvan för y = skovelns
avloppsvinkel ß. Vi få således en första gren av
avlopps-förlustkurvan såsom en parabel.
II. Avloppsförlusten vid ha stig heter
över ljudhastigheten.
Inom det fuktiga området, där vi vanligen röra oss,
är ljudhastigheten ca 380 m/sek., och den inritade
kurvan för w2 — 380 m/sek. varskor oss om, när vi
nalkas resp. överskrida denna gräns.
Saken blir då vansklig, ty inträffa då
efterexpan-sioner i skovelns sneddavlopp, som medföra
riktningsändringar av strålen, så att y blir skild från ß,
därigenom att den erforderliga areaförstoringen
uppnås först genom en avlänkning av strålen med <5,
dvs. 6 = y —• ß.
För att söka något uppklara huru förhållandena
gestalta sig vid dessa överljudhastigheter, förutsättes
att vid sista skoveln relativa inloppshastigheten är
mindre än ljudhastigheten.
Enligt termodynamiken kan då i skovelns trängsta
sektion aldrig större relativ hastighet än
ljudhastigheten w, uppstå. Storleken av ljudhastigheten är,
om tillståndet i minsta sektionen förses med index m,
u>im = \fàg Pm vm
där k är exponenten för adiabaten, vilken inom det
fuktiga området någorlunda kan sättas vid specifika
ångmängden x
k — 1,035 + 0,1 x.
Vid uppträdande av ljudhastigheten erhålles således
ångströmmen Å genom skoveln av
Å-
v
kg– (kg/sek).
Pm -0.577.
üt
Pm
Pz
pt ■ 0,577
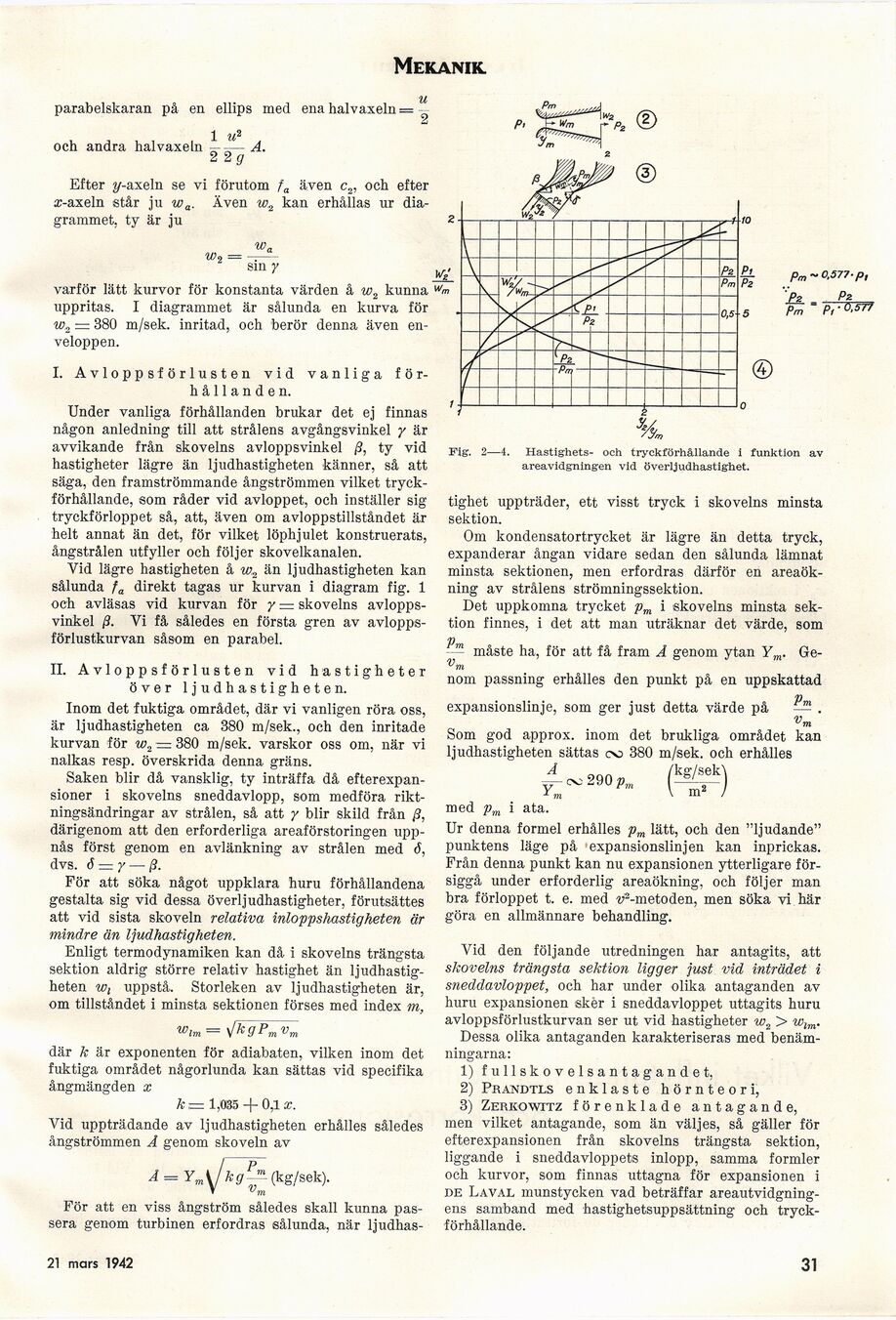
Fig.
-4. Hastighets- och tryckförhållande i funktion av
areavidgningen vid överljudhastighet.
För att en viss ångström således skall kunna
passera genom turbinen erfordras sålunda, när ljudhas-
tighet uppträder, ett visst tryck i skovelns minsta
sektion.
Om kondensatortrycket är lägre än detta tryck,
expanderar ångan vidare sedan den sålunda lämnat
minsta sektionen, men erfordras därför en
areaökning av strålens strömningssektion.
Det uppkomna trycket pm i skovelns minsta
sektion finnes, i det att man uträknar det värde, som
V
- — måste ha, för att få fram Å genom ytan Ym. Ge-
nom passning erhålles den punkt på en uppskattad
V
expansionslinje, som ger just detta värde på — .
vm
Som god approx. inom det brukliga området kan
ljudhastigheten sättas oo 380 m/sek. och erhålles
med pm i ata.
Ur denna formel erhålles pm lätt, och den "ljudande"
punktens läge på expansionslinjen kan inprickas.
Från denna punkt kan nu expansionen ytterligare
försiggå under erforderlig areaökning, och följer man
bra förloppet t. e. med v2-metoden, men söka vi här
göra en allmännare behandling.
Vid den följande utredningen har antagits, att
skovelns trängsta sektion ligger just vid inträdet i
sneddavloppet, och har under olika antaganden av
huru expansionen skèr i sneddavloppet uttagits huru
avloppsförlustkurvan ser ut vid hastigheter w2 > w,m.
Dessa olika antaganden karakteriseras med
benämningarna:
1) fullskovelsantagandet,
2) Prandtls enklaste hörnteori,
3) Zerkowitz förenklade antagande,
men vilket antagande, som än väljes, så gäller för
efterexpansionen från skovelns trängsta sektion,
liggande i sneddavloppets inlopp, samma formler
och kurvor, som finnas uttagna för expansionen i
de Laval munstycken vad beträffar
areautvidgningens samband med hastighetsuppsättning och
tryck-förhållande.
21 mars 1942
31
<< prev. page << föreg. sida << >> nästa sida >> next page >>