
Full resolution (JPEG) - On this page / på denna sida - H. 37. 14 september 1946 - Leibniz — ett trehundraårsminne inom matematiken, av Eric von Born
<< prev. page << föreg. sida << >> nästa sida >> next page >>
Below is the raw OCR text
from the above scanned image.
Do you see an error? Proofread the page now!
Här nedan syns maskintolkade texten från faksimilbilden ovan.
Ser du något fel? Korrekturläs sidan nu!
This page has never been proofread. / Denna sida har aldrig korrekturlästs.
874
TEKNISK TIDSKRIFT
clar alla så att säga löpte samman i en enda hand.
Differentialräkningen skulle kort efter Leibniz’
dagar erövra världen, och dess herravälde har
fram till i dag upprätthållits på basen av den
kända "Leibnizformeln" (fig. 2).
En annan frukt av Leibniz’ första vistelse i den
franska metropolen var Leibnizserien, härledd ur
arcustangensfunktionen. Den utgör i princip en
oändlig sicksacklinje och kan för x •= 1 skrivas
= 4_44_ 4_4o. 4_
71 ~ 1 3 5 7 2/i — 1
Därefter löste Leibniz det dubbla
tangentproblemet, och därmed togs ett långt steg framåt på
den bana, där matematiken nu kunde företa ett
kosmiskt erövringståg. Fakta ge visserligen vid
handen, att Newton redan år 1665 kommit på
infinitesimalkalkylen, alltså ett decennium före
Leibniz, och att den senare först 1684 i sin
tidskrift ’"Acta Eruditorum" framlagt den för
offentligheten. men noggranna undersökningar av
Newtons och Leibniz’ efterlämnade papper samt av
annat primärt källmaterial ge obestridligt vid
handen, att de båda matematiska snillena
oberoende av varandra och i tysthet gått fram i
ungefär samma riktning på forskningens väg, så att
ingen anledning finnes att här förmoda något
plagiat. Denna uppfattning bestyrkes även av den
omständigheten, att Newton använde sin upptäckt
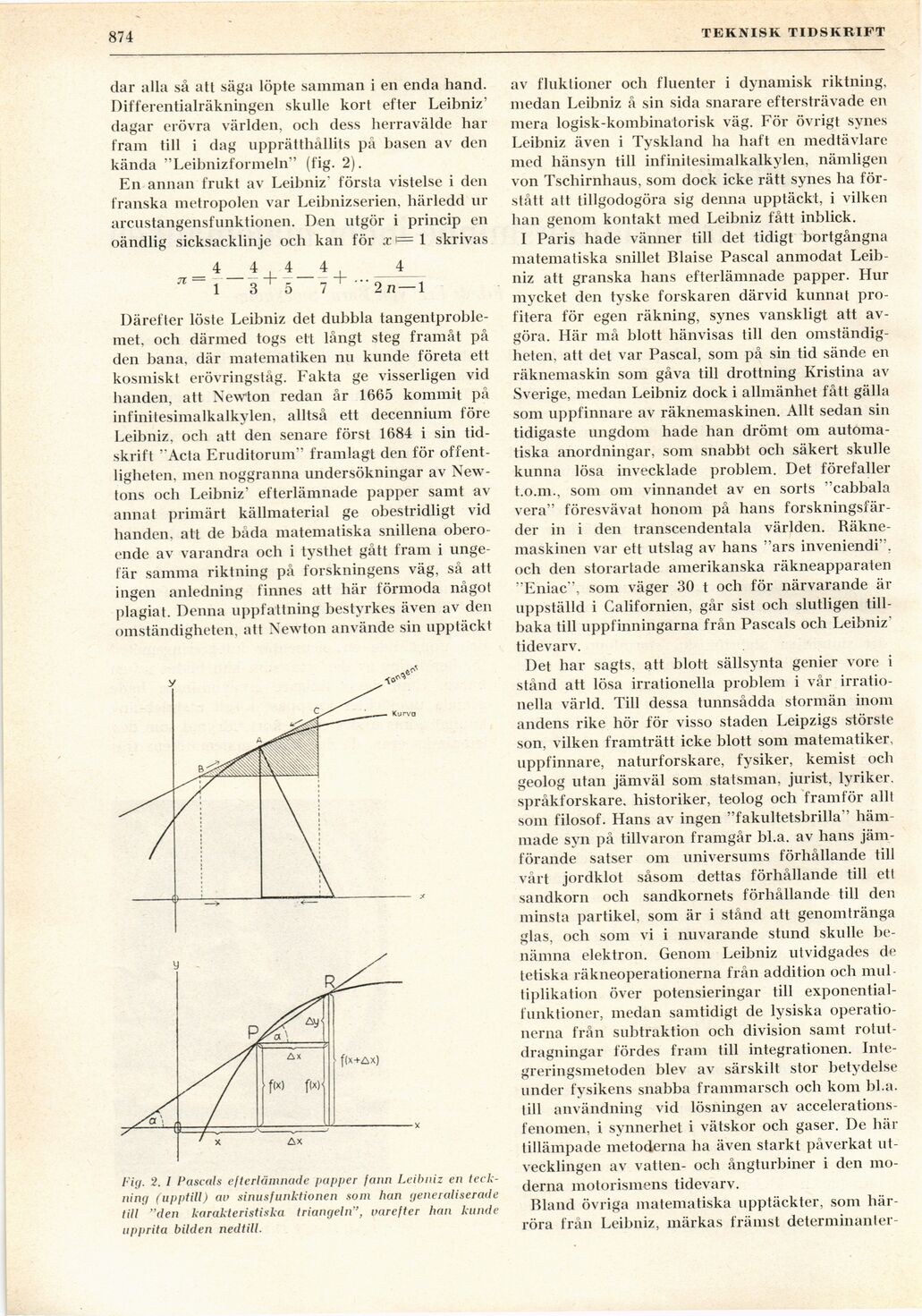
Fig. 2. I Pascals efterlämnade papper fann Leibniz en
teckning (upptill) av sinusfunktionen som han generaliserade
till "den karakteristiska triangeln’’, varefter han kunde
upprita bilden nedtill.
av fluktioner och fluenter i dynamisk riktning,
medan Leibniz å sin sida snarare eftersträvade en
mera logisk-kombinatorisk väg. För övrigt synes
Leibniz även i Tyskland ha haft en medtävlare
med hänsyn till infinitesimalkalkylen, nämligen
von Tschirnhaus, som dock icke rätt synes ha
förstått att tillgodogöra sig denna upptäckt, i vilken
ban genom kontakt med Leibniz fått inblick.
I Paris hade vänner till det tidigt bortgångna
matematiska snillet Blaise Pascal anmodat
Leibniz att granska hans efterlämnade papper. Hur
mycket den tyske forskaren därvid kunnat
profitera för egen räkning, synes vanskligt att
avgöra. Här må blott hänvisas till den
omständigheten. att det var Pascal, som på sin tid sände en
räknemaskin som gåva till drottning Kristina av
Sverige, medan Leibniz dock i allmänhet fått gälla
som uppfinnare av räknemaskinen. Allt sedan sin
tidigaste ungdom hade han drömt om
automatiska anordningar, som snabbt och säkert skulle
kunna lösa invecklade problem. Det förefaller
t.o.m., som om vinnandet av en sorts "cabbala
vera" föresvävat honom på hans
forskningsfärder in i den transcendentala världen.
Räknemaskinen var ett utslag av hans "ars inveniendi".
och den storartade amerikanska räkneapparaten
"Eniac", som väger 30 t och för närvarande är
uppställd i Californien, går sist och slutligen
tillbaka till uppfinningarna från Pascals och Leibniz’
tidevarv.
Det har sagts, att blott sällsynta genier vore i
stånd att lösa irrationella problem i vår
irrationella värld. Till dessa tunnsådda stormän inom
andens rike hör för visso staden Leipzigs störste
son, vilken framträtt icke blott som matematiker,
uppfinnare, naturforskare, fysiker, kemist och
geolog utan jämväl som statsman, jurist, lyriker,
språkforskare, historiker, teolog och framför allt
som filosof. Hans av ingen "fakultetsbrilla"’
hämmade syn på tillvaron framgår bl.a. av hans
jämförande satser om universums förhållande till
vårt jordklot såsom dettas förhållande till ett
sandkorn och sandkornets förhållande till den
minsta partikel, som är i stånd att genomtränga
glas, och som vi i nuvarande stund skulle
benämna elektron. Genom Leibniz utvidgades de
tetiska räkneoperationerna från addition och
multiplikation över potensieringar till
exponential-funktioner, medan samtidigt de lysiska
operationerna från subtraktion och division samt
rotut-dragningar fördes fram till integrationen.
Integreringsmetoden blev av särskilt stor betydelse
under fysikens snabba frammarsch och kom bl.a.
till användning vid lösningen av
accelerationsfenomen, i synnerhet i vätskor och gaser. De här
tillämpade metoderna ha även starkt påverkat
utvecklingen av vatten- och ångturbiner i den
moderna motorismens tidevarv.
Bland övriga matematiska upptäckter, som
härröra från Leibniz, märkas främst determinanter-
<< prev. page << föreg. sida << >> nästa sida >> next page >>