
Full resolution (JPEG) - On this page / på denna sida - Grundläggande vetenskaper, av Olof Lodén - Matematik - 141. Koordinatsystem
<< prev. page << föreg. sida << >> nästa sida >> next page >>
Below is the raw OCR text
from the above scanned image.
Do you see an error? Proofread the page now!
Här nedan syns maskintolkade texten från faksimilbilden ovan.
Ser du något fel? Korrekturläs sidan nu!
This page has never been proofread. / Denna sida har aldrig korrekturlästs.
Matematik
141. Koordinatsystem.
Rätvinkliga koordinater.
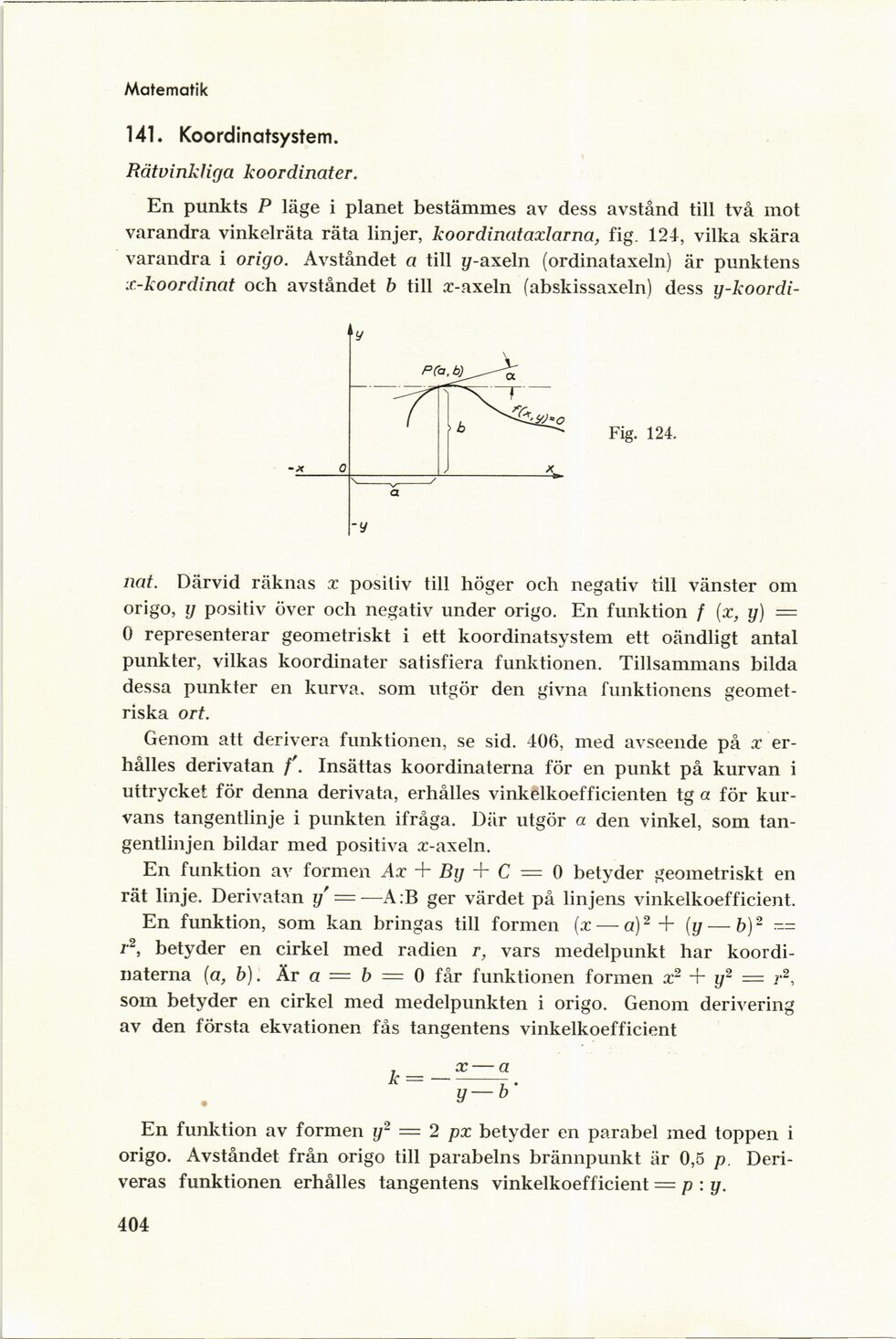
En punkts P läge i planet bestämmes av dess avstånd till två mot
varandra vinkelräta räta linjer, koordinataxlarna, fig. 124, vilka skära
varandra i origo. Avståndet a till y-axeln (ordinataxeln) är punktens
x-koordinat och avståndet b till x-axeln (abskissaxeln) dess y-koordi-
nat. Därvid räknas x positiv till höger och negativ till vänster om
origo, y positiv över och negativ under origo. En funktion f (x, y) =
0 representerar geometriskt i ett koordinatsystem ett oändligt antal
punkter, vilkas koordinater satisfiera funktionen. Tillsammans bilda
dessa punkter en kurva, som utgör den givna funktionens
geometriska ort.
Genom att derivera funktionen, se sid. 406, med avseende på x
erhålles derivatan f. Insättas koordinaterna för en punkt på kurvan i
uttrycket för denna derivata, erhålles vinkelkoefficienten tg a för
kurvans tangentlinje i punkten ifråga. Där utgör a den vinkel, som
tangentlinjen bildar med positiva x-axeln.
En funktion av formen Ax + By + C = 0 betyder geometriskt en
rät linje. Derivatan y’ = —A.B ger värdet på linjens vinkelkoefficient.
En funktion, som kan bringas till formen (x — a)2 + (y — b)2 =
r2, betyder en cirkel med radien r, vars medelpunkt har
koordinaterna (a, b). Är a = b = 0 får funktionen formen x? + y2 = r2,
som betyder en cirkel med medelpunkten i origo. Genom derivering
av den första ekvationen fås tangentens vinkelkoefficient
k = -
x— a
y—b‘
En funktion av formen y2 = 2 px betyder en parabel med toppen i
origo. Avståndet från origo till parabelns brännpunkt är 0,5 p.
Deri-veras funktionen erhålles tangentens vinkelkoefficient = p : y.
404
Fig. 124.
<< prev. page << föreg. sida << >> nästa sida >> next page >>